
Using parent graphs to understand the left and right hand limits
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value

Percentiles, Deciles, Quartiles
Understanding percentiles, quartiles, and deciles through definitions and examples
From playlist Unit 1: Descriptive Statistics
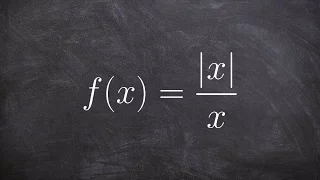
Learn how to evaluate left and right hand limits of a function
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value

How to evaluate the limit of a function by observing its graph
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value

Math 101 091117 Introduction to Analysis 05 Absolute Value
Absolute value: definition. Notion of distance. Properties of the absolute value: proofs. Triangle inequality
From playlist Course 6: Introduction to Analysis (Fall 2017)

Evaluate the limit for a value of a function
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value

Absolute versus relative measurements in geometry | Rational Geometry Math Foundations 134
In science and ordinary life, the distinction between absolute and relative measurements is very useful. It turns out that in mathematics this is also an important distinction. We must be prepared that some aspects of mathematics are more naturally measured relatively, rather than absolute
From playlist Math Foundations

Evaluate the left and right hand limit by graphing the function
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value

Mark Meckes: Magnitude and intrinsic volumes in subspaces of L1
Magnitude is an isometric invariant of metric spaces, with origins in category theory, which turns out to be related to a wide variety of classical geometric invariants, including Minkowski dimension, volume, and surface measure. For convex bodies in ln1 , magnitude turns out to be an l1 a
From playlist Workshop: High dimensional measures: geometric and probabilistic aspects

Christina Sormani: A Course on Intrinsic Flat Convergence part 1
Intrinsic Flat Convergence was first introduced in joint work with Stefan Wenger building upon work of Ambrosio-Kirchheim to address a question proposed by Tom Ilmanen. In this talk, I will present an overview of the initial paper on the topic [JDG 2011]. I will briefly describe key examp
From playlist HIM Lectures 2015

C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 1 (version temporaire)
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with uniform lower bounds on their scalar curvature. We close the course by presenting methods and the
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Antoine Song - Spherical Plateau problem and applications
I will discuss an area minimization problem in certain quotients of the Hilbert sphere by countable groups. An early version of that setting appears in Besson-Courtois-Gallot’s work on the entropy inequality. As an application of this minimization problem, we obtain some stability results.
From playlist Not Only Scalar Curvature Seminar

Micrometer/diameter of daily used objects.
What was the diameter? music: https://www.bensound.com/
From playlist Fine Measurements

C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 1
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with uniform lower bounds on their scalar curvature. We close the course by presenting methods and the
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Stability of the spacetime positive mass theorem in spherical symmetry - Marcus Khuri
More videos on http://video.ias.edu
From playlist Mathematics

Elchanan Solomon (10/16/18): An intrinsic persistent homology transform
The Persistent Homology Transform (PHT) and Euler Characteristic Transform (ECT), first proposed by Turner, Mukherjee, and Boyer, were the first TDA invariants shown to be injective on the space of shapes embedded in Euclidean space. A number of recent papers have presented new, elegant ne
From playlist AATRN 2018

Andreas Bernig: Intrinsic volumes on pseudo-Riemannian manifolds
The intrinsic volumes in Euclidean space can be defined via Steiner’s tube formula and were characterized by Hadwiger as the unique continuous, translation and rotation invariant valuations. By the Weyl principle, their extension to Riemannian manifolds behaves naturally under isometric em
From playlist Workshop: High dimensional measures: geometric and probabilistic aspects

Christina Sormani - Currents on metric spaces and intrinsic flat convergence
First I will provide a brief introduction to Ambrosio-Kirchheim’s Theory of Currents on Metric Spaces. Then I will review joint work with Wenger defining integral current spaces and intrinsic flat convergence. This will provide sufficient background needed to follow the talk of Antoine Son
From playlist Not Only Scalar Curvature Seminar
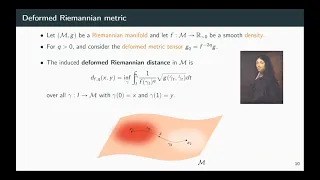
Ximena Fernández - Intrinsic persistent homology via density-based metric learning
38th Annual Geometric Topology Workshop (Online), June 15-17, 2021 Ximena Fernández, Swansea University Title: Intrinsic persistent homology via density-based metric learning Abstract: Typically, persistence diagrams computed from a sample depend strongly on the distance associated to th
From playlist 38th Annual Geometric Topology Workshop (Online), June 15-17, 2021

Evaluate the limit of an absolute value function by direct substitution
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value