Proof by infinite descent

Mathematical proofs | Diophantine equations | Mathematical terminology

In mathematics, a proof by infinite descent, also known as Fermat's method of descent, is a particular kind of proof by contradiction used to show that a statement cannot possibly hold for any number, by showing that if the statement were to hold for a number, then the same would be true for a smaller number, leading to an infinite descent and ultimately a contradiction. It is a method which relies on the well-ordering principle, and is often used to show that a given equation, such as a Diophantine equation, has no solutions. Typically, one shows that if a solution to a problem existed, which in some sense was related to one or more natural numbers, it would necessarily imply that a second solution existed, which was related to one or more 'smaller' natural numbers. This in turn would imply a third solution related to smaller natural numbers, implying a fourth solution, therefore a fifth solution, and so on. However, there cannot be an infinity of ever-smaller natural numbers, and therefore by mathematical induction, the original premise—that any solution exists— is incorrect: its correctness produces a contradiction. An alternative way to express this is to assume one or more solutions or examples exists, from which a smallest solution or example—a minimal counterexample—can then be inferred. Once there, one would try to prove that if a smallest solution exists, then it must imply the existence of a smaller solution (in some sense), which again proves that the existence of any solution would lead to a contradiction. The earliest uses of the method of infinite descent appear in Euclid's Elements. A typical example is Proposition 31 of Book 7, in which Euclid proves that every composite integer is divided (in Euclid's terminology "measured") by some prime number. The method was much later developed by Fermat, who coined the term and often used it for Diophantine equations. Two typical examples are showing the non-solvability of the Diophantine equation r2 + s4 = t4 and proving Fermat's theorem on sums of two squares, which states that an odd prime p can be expressed as a sum of two squares when p ≡ 1 (mod 4) (see proof). In this way Fermat was able to show the non-existence of solutions in many cases of Diophantine equations of classical interest (for example, the problem of four perfect squares in arithmetic progression). In some cases, to the modern eye, his "method of infinite descent" is an exploitation of the inversion of the doubling function for rational points on an elliptic curve E. The context is of a hypothetical non-trivial rational point on E. Doubling a point on E roughly doubles the length of the numbers required to write it (as number of digits), so that a "halving" a point gives a rational with smaller terms. Since the terms are positive, they cannot decrease forever. (Wikipedia).

IMO 1988 Question 6 [TL;DR version] (proof by infinite descent)

From the 1988 International Maths Olympiad. If you want to see more problems like this check out the IMO website - https://www.imo-official.org/default.aspx Edit (4/10/2020) - I have realised this proof is actually incomplete. The general method is okay, but I missed a small detail. I n

From playlist Problem Solving

Infinite Series: The Ratio Test I

This video provides an example of how to determine if an infinite series converges or diverges using the ratio test. Site: http://mathispower4u.com Blog: http://mathispower4u.com

From playlist Infinite Series

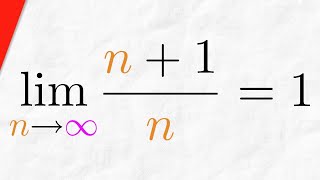
Proof: Sequence (n+1)/n Converges to 1 | Real Analysis

We will prove the sequence (n+1)/n converges to 1. In other words, we're proving that the limit of (n+1)/n as n approaches infinity is 1. We use the epsilon definition of a convergent sequence and the proof is straightforward, following the typical form of a convergent sequence proof. Re

From playlist Real Analysis

Ex 4: Infinite Series - The Root Test (Convergent) e^(bn)n^n

This video explains how to determine if an infinite series is convergent or divergent using the Root Test. Form: e^(bn)/n^n Site: http://mathispower4u.com

From playlist Infinite Series

Ex: Infinite Series - Integral Test Requiring Integration by Parts (Convergent)

This video explains how to apply the Integral Test to determine if an infinite series is convergent or divergent. Site: http://mathispower4u.com

From playlist Infinite Series

Ex 1: Infinite Series - P Series Test (Convergent) and Find a Partial Sum

This video explains how to apply the p-series test to determine if an infinite series is convergent or divergent. Site: http://mathispower4u.com

From playlist Infinite Series

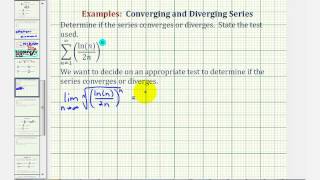
Infinite Series: The Root Test I

This video provides an example of how to determine if an infinite series converges or diverges using the root test. Site: http://mathispower4u.com Blog: http://mathispower4u.com

From playlist Infinite Series

How to Prove a Sequence with Two Components Converges

How to Prove a Sequence with Two Components Converges If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)

From playlist Advanced Calculus

Infinite Products of Projective Schemes Don't Exist

In this video we explain why infinite products of projective schemes don't exist as objects in the category of schemes.

From playlist Schemes

Optimal machine learning with stochastic projections (...) - Rosasco - Workshop 3 - CEB T1 2019

Lorenzo Rosasco (MIT-IIT) / 03.04.2019 Optimal machine learning with stochastic projections and regularization. Projecting data in low dimensions is often key to scale machine learning to large high-dimensional data-sets. In this talk we will take take a statistical learning tour of cla

From playlist 2019 - T1 - The Mathematics of Imaging

Margins, perceptrons, and deep networks - Matus Telgarsky

Seminar on Theoretical Machine Learning Topic: Margins, perceptrons, and deep networks Speaker: Matus Telgarsky-2020-03-26 Affiliation: University of Illinois Date: March 26, 2020 For more video please visit http://video.ias.edu

From playlist Mathematics

Infinite Series: The Alternating Series Test

This video provides an examples of how to apply the alternating series test to determine if a infinite series is convergent or divergent. Site: http://mathispower4u.com Blog: http://mathispower4u.wordpress.com

From playlist Infinite Series

Andrew Wiles: Fermat's Last theorem: abelian and non-abelian approaches

The successful approach to solving Fermat's problem reflects a move in number theory from abelian to non-abelian arithmetic. This lecture was held by Abel Laurate Sir Andrew Wiles at The University of Oslo, May 25, 2016 and was part of the Abel Prize Lectures in connection with the Abel P

From playlist Sir Andrew J. Wiles

Is Optimization the Right Language to Understand Deep Learning? - Sanjeev Arora

Workshop on Theory of Deep Learning: Where Next? Topic: Is Optimization the Right Language to Understand Deep Learning? Speaker: Sanjeev Arora Affiliation: Princeton University; Distinguished Visiting Professor, School of Mathematics Date: October 15, 2019 For more video please visit ht

From playlist ML @ Scale

The golden ratio spiral: visual infinite descent

NEW (Christmas 2019). Two ways to support Mathologer Mathologer Patreon: https://www.patreon.com/mathologer Mathologer PayPal: paypal.me/mathologer (see the Patreon page for details) So you all know the golden (ratio) spiral. But did you know that not only the golden ratio but really ev

From playlist Recent videos

Taylor Dupuy 5/9/14 Part 1

Title: Jet Spaces and Diophantine Problems

From playlist Spring 2014

Nima Rasekh - Every Elementary Higher Topos has a Natural Number Object

Talk at the school and conference “Toposes online” (24-30 June 2021): https://aroundtoposes.com/toposesonline/ Slides: https://aroundtoposes.com/wp-content/uploads/2021/07/NimaSlidesToposesOnline.pdf One key aspect of elementary topos theory is the existence of a natural number object. W

From playlist Toposes online

Ex 5: Infinite Series - The Root Test (Divergent) (n/c)^n

This video explains how to determine if an infinite series is convergent or divergent using the Root Test. Form: (n/c)^n Site: http://mathispower4u.com

From playlist Infinite Series

Tongmu He - Sen operators and Lie algebras arising from Galois representations over p-adic varieties

Any finite-dimensional p-adic representation of the absolute Galois group of a p-adic local field with imperfect residue field is characterized by its arithmetic and geometric Sen operators defined by Sen-Brinon. We generalize their construction to the fundamental group of a p-adic affine

From playlist Franco-Asian Summer School on Arithmetic Geometry (CIRM)

Proof by infinite descent

Related pages