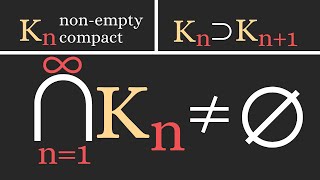Theorems in real analysis | Sets of real numbers
Nested intervals
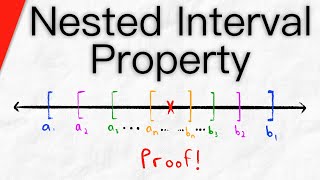
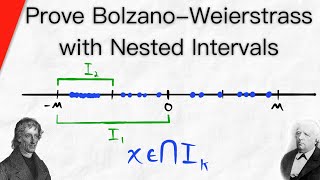
In mathematics, a sequence of nested intervals can be intuitively understood as an ordered collection of intervals on the real number line with natural numbers as an index. In order for a sequence of intervals to be considered nested intervals, two conditions have to be met: 1. * Every interval in the sequence is contained in the previous one ( is always a subset of ). 2. * The length of the intervals get arbitrarily small (meaning the length falls below every possible threshold after a certain index ). In other words, the left bound of the interval can only increase, and the right bound can only decrease. Historically - long before anyone defined nested intervals in a textbook - people implicitly constructed such nestings for concrete calculation purposes. For example, the ancient Babylonians discovered a method for computing square roots of numbers. In contrast, the famed Archimedes constructed sequences of polygons, that inscribed and surcumscribed a unit circle, in order to get a lower and upper bound for the circles circumference - which is the circle number Pi. The central question to be posed is the nature of the intersection over all the natural numbers, or, put differently, the set of numbers, that are found in every Interval (thus, for all ). In modern mathematics, nested intervals are used as a construction method for the real numbers (in order to complete the field of rational numbers). (Wikipedia).