
Modular Forms | Modular Forms; Section 1 2
We define modular forms, and borrow an idea from representation theory to construct some examples. My Twitter: https://twitter.com/KristapsBalodi3 Fourier Theory (0:00) Definition of Modular Forms (8:02) In Search of Modularity (11:38) The Eisenstein Series (18:25)
From playlist Modular Forms

This lecture is part of an online graduate course on modular forms. We introduce modular forms, and give several examples of how they were used to solve problems in apparently unrelated areas of mathematics. I will not be following any particular book, but if anyone wants a suggestion
From playlist Modular forms

Modular forms: Eisenstein series
This lecture is part of an online graduate course on modular forms. We give two ways of looking at modular forms: as functions of lattices in C, or as invariant forms. We use this to give two different ways of constructing Eisenstein series. For the other lectures in the course see http
From playlist Modular forms

Modular Functions | Modular Forms; Section 1.1
In this video we introduce the notion of modular functions. My Twitter: https://twitter.com/KristapsBalodi3 Intro (0:00) Weakly Modular Functions (2:10) Factor of Automorphy (8:58) Checking the Generators (15:04) The Nome Map (16:35) Modular Functions (22:10)
From playlist Modular Forms

This lecture is part of an online graduate course on modular forms. We first show that the number of zeros of a (level 1 holomorphic) modular form in a fundamental domain is weight/12, and use this to show that the graded ring of modular forms is the ring of polynomials in E4 and E6. Fo
From playlist Modular forms

p-adic modular forms - Christian Johansson
Short Talks by Postdoctoral Members Christian Johansson - September 29, 2015 http://www.math.ias.edu/calendar/event/88274/1443550500/1443551400 More videos on http://video.ias.edu
From playlist Short Talks by Postdoctoral Members

Modular forms: Theta functions
This lecture is part of an online graduate course on modular forms. We show that the theta function of a 1-dimensional lattice is a modular form using the Poisson summation formula, and use this to prove the functional equation of the Riemann zeta function. For the other lectures in th
From playlist Modular forms

Modular forms: Modular functions
This lecture is part of an online graduate course on modular forms. We classify all meromorphic modular functions, showing that they are all rational functions of the elliptic modular function j. As an application of j we use it to prove Picard's theorem that a non-constant meromorphic
From playlist Modular forms

Introduction to Modular Forms - Part 3 of 8
“Introduction to Modular Forms,” by Keith Conrad. Topics include Eisenstein series and q-expansions, applications to sums of squares and zeta-values, Hecke operators, eigenforms, and the L-function of a modular form. This is a video from CTNT, the Connecticut Summer School in Number Theor
From playlist CTNT 2016 - "Introduction to Modular Forms" by Keith Conrad

Counting points on the E8 lattice with modular forms (theta functions) | #SoME2
In this video, I show a use of modular forms to answer a question about the E8 lattice. This video is meant to serve as an introduction to theta functions of lattices and to modular forms for those with some knowledge of vector spaces and series. -------------- References: (Paper on MIT
From playlist Summer of Math Exposition 2 videos

Modular forms and multiple q-Zeta values (Lecture 2) by Ulf Kuehn
PROGRAM : ALGEBRAIC AND ANALYTIC ASPECTS OF AUTOMORPHIC FORMS ORGANIZERS : Anilatmaja Aryasomayajula, Venketasubramanian C G, Jurg Kramer, Dipendra Prasad, Anandavardhanan U. K. and Anna von Pippich DATE & TIME : 25 February 2019 to 07 March 2019 VENUE : Madhava Lecture Hall, ICTS Banga
From playlist Algebraic and Analytic Aspects of Automorphic Forms 2019
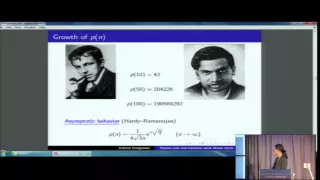
Dyson's Rank, Harmonic Weak Maass Form, and Recent Developments - Kathrin Bringmann
Kathrin Bringmann University of Cologne September 27, 2013 More videos on http://video.ias.edu
From playlist Dreams of Earth and Sky

DISCUSSION MEETING SPHERE PACKING ORGANIZERS: Mahesh Kakde and E.K. Narayanan DATE: 31 October 2019 to 06 November 2019 VENUE: Madhava Lecture Hall, ICTS Bangalore Sphere packing is a centuries-old problem in geometry, with many connections to other branches of mathematics (number the
From playlist Sphere Packing - 2019
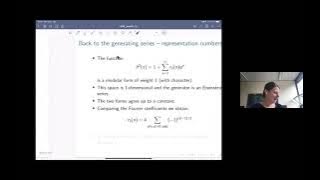
Claudia Alfes: Traces of CM values and geodesic cycle integrals of modular functions
In this talk we give an introduction to the study of generating series of the traces of CM values and geodesic cycle integrals of different modular functions. First we define modular forms and harmonic Maass forms. Then we briefly discuss the theory of theta lifts that gives a conceptual f
From playlist Seminar Series "Arithmetic Applications of Fourier Analysis"

Serre's Conjecture for GL_2 over Totally Real Fields (Lecture 4) by Fred Diamond
Program Recent developments around p-adic modular forms (ONLINE) ORGANIZERS: Debargha Banerjee (IISER Pune, India) and Denis Benois (University of Bordeaux, France) DATE: 30 November 2020 to 04 December 2020 VENUE: Online This is a follow up of the conference organized last year arou
From playlist Recent Developments Around P-adic Modular Forms (Online)

Serre's Conjecture for GL_2 over Totally Real Fields (Lecture 2) by Fred Diamond
Program Recent developments around p-adic modular forms (ONLINE) ORGANIZERS: Debargha Banerjee (IISER Pune, India) and Denis Benois (University of Bordeaux, France) DATE: 30 November 2020 to 04 December 2020 VENUE: Online This is a follow up of the conference organized last year arou
From playlist Recent Developments Around P-adic Modular Forms (Online)

Modular forms: Theta functions in higher dimensions
This lecture is part of an online graduate course on modular forms. We study theta functions of even unimodular lattices, such as the root lattice of the E8 exceptional Lie algebra. As examples we show that one cannot "her the shape of a drum", and calculate the number of minimal vectors
From playlist Modular forms

An algebro-geometric theory of vector-valued modular forms of half-integral weight - Luca Candelori
Luca Candelori Lousiana State University October 23, 2014 We give a geometric theory of vector-valued modular forms attached to Weil representations of rank 1 lattices. More specifically, we construct vector bundles over the moduli stack of elliptic curves, whose sections over the complex
From playlist Mathematics