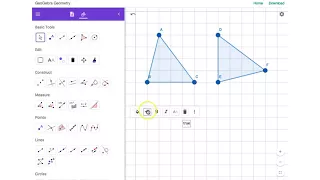
Introducing the Concept of Congruence
From playlist GeoGebra Geometry

Introduction to Congruent Triangles
Complete videos list: http://mathispower4u.yolasite.com/ This video will define congruent triangles and state the ways to prove two triangles are congruent.
From playlist Triangles and Congruence

Number Theory | Congruence Modulo n -- Definition and Examples
We define the notion of congruence modulo n among the integers. http://www.michael-penn.net
From playlist Modular Arithmetic and Linear Congruences

Triangle Congruence (quick review)
More resources available at www.misterwootube.com
From playlist Further Properties of Geometrical Figures

In this video we continue discussing congruences and, in particular, we discuss solutions of linear congruences. The content of this video corresponds to Section 4.4 of my book "Number Theory and Geometry" which you can find here: https://alozano.clas.uconn.edu/number-theory-and-geometry/
From playlist Number Theory and Geometry
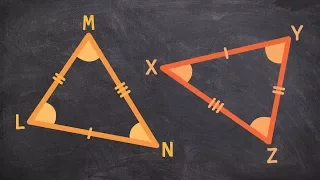
What is the Definition of Congruent Triangles - Congruent Triangles
👉 Learn about congruent triangles theorems. Two or more triangles (or polygons) are said to be congruent if they have the same shape and size. There are many methods to determine whether two triangles are congruent. Some of the methods include: (1) The SSS (Side Side Side) congruency the
From playlist Congruent Triangles

What is an Included Side of a Triangle - Congruent Triangles
👉 Learn about the included angles of a triangle. An included angle of a triangle is the angle between two sides of a triangle. An included side of a triangle is the side between two angles. To show that two triangles are congruent by the side angle side (SAS) congruency theorem, we must s
From playlist Congruent Triangles

Number Theory | Some properties of integer congruence.
We examine some basic properties of congruence modulo n among the integers.
From playlist Modular Arithmetic and Linear Congruences

Angelica Babei - A family of $\phi$-congruence subgroups of the modular group
In this talk, we introduce families of subgroups of finite index in the modular group, generalizing the congruence subgroups. One source of such families is studying homomorphisms of the modular group into linear algebraic groups over finite fields. In particular, we examine a family of no
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Profinite Completions and Representation Rigidity - Ryan Spitler
Arithmetic Groups Topic: Profinite Completions and Representation Rigidity Speaker: Ryan Spitler Affiliation: Rice University Date: February 02, 2022 Taking up the terminology established in the first lecture, in 1970 Grothendieck showed that when two groups (G,H) form a Grothendieck pai
From playlist Mathematics

Congruence Modulo n Arithmetic Properties: Equivalent Relation
This video explains the properties of congruence modulo which makes it an equivalent relation. mathispower4u.com
From playlist Additional Topics: Generating Functions and Intro to Number Theory (Discrete Math)

The congruence subgroup property for SL(2,Z) - William Yun Chen
Arithmetic Groups Topic: The congruence subgroup property for SL(2,Z) Speaker: William Yun Chen Affiliation: Member, School of Mathematics Date: November 10, 2021 Somehow, despite the title, SL(2,Z) is the poster child for arithmetic groups not satisfying the congruence subgroup property
From playlist Mathematics

Prasad's work on the congruence subgroup problem by Andrei Rapinchuk
PROGRAM ZARISKI-DENSE SUBGROUPS AND NUMBER-THEORETIC TECHNIQUES IN LIE GROUPS AND GEOMETRY (ONLINE) ORGANIZERS: Gopal Prasad, Andrei Rapinchuk, B. Sury and Aleksy Tralle DATE: 30 July 2020 VENUE: Online Unfortunately, the program was cancelled due to the COVID-19 situation but it will
From playlist Zariski-dense Subgroups and Number-theoretic Techniques in Lie Groups and Geometry (Online)
Tim Steger: Construction of lattices defining fake projective planes - lecture 8
Recording during the meeting "Ball Quotient Surfaces and Lattices " the March 01, 2019 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathe
From playlist Algebraic and Complex Geometry

Congruence Subgroup Problem by M. S. Raghunathan
PROGRAM SMOOTH AND HOMOGENEOUS DYNAMICS ORGANIZERS: Anish Ghosh, Stefano Luzzatto and Marcelo Viana DATE: 23 September 2019 to 04 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Ergodic theory has its origins in the the work of L. Boltzmann on the kinetic theory of gases.
From playlist Smooth And Homogeneous Dynamics

Applications to modular forms and noncongruence arithmetic groups - Yunqing Tang and Frank Calegari
Arithmetic Groups Topic: Applications to modular forms and noncongruence arithmetic groups Speakers: Yunqing Tang and Frank Calegari Affiliation: Princeton University; University of Chicago Date: December 01, 2021 We explain our proof of the unbounded denominators conjecture. This talk
From playlist Mathematics

Diophantine analysis in thin orbits - Alex Kontorovich
Special Seminar Topic: Diophantine analysis in thin orbits Speaker: Alex Kontorovich Affiliation: Rutgers University; von Neumann Fellow, School of Mathematics Date: December 8, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Groups with bounded generation: old and new - Andrei S. Rapinchuk
Joint IAS/Princeton University Number Theory Seminar Topic: Groups with bounded generation: old and new Speaker: Andrei S. Rapinchuk Date: May 06, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

Do you know the five tests for congruent triangles? In this video I explain congruence and go through some example problems. anime opening: https://www.youtube.com/watch?v=m1GIFsT5Yng
From playlist Geometry Revision

Mod By A Group: Generalized Modular Arithmetic, from Basic Modular Arithmetic Congruence to 'Normal'
This time I wanted to tackle what it means to Mod by a Group (or rather by a subgroup) and how that can give rise to generalized modular arithmetic. I start from basic modular arithmetic congruence in the integers and used that as a vehicle to build up to the idea of 'Normal' in Abstract a
From playlist The New CHALKboard