
How to construct the Leech lattice
This lecture describes an astonishingly simple construction of the Leech lattice in 24 dimensions, found by John Conway and Neal Sloane. This is an experimental joint video with @Lyam Boylan (https://www.tiktok.com/@yamsox/video/7057530890381053189) who added the animation, the thumbnai
From playlist Math talks

History of science 7: Did Witt discover the Leech lattice?
In about 1970 the German mathematician Witt claimed to have discovered the Leech lattice many years before Leech. This video explains what the Leech lattice is and examines the evidence for Witt's claim. Lieven Lebruyn discussed this question on his blog: http://www.neverendingbooks.org/w
From playlist History of science
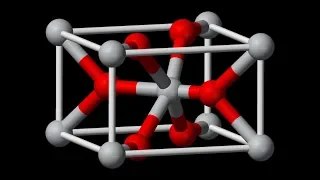
Lattice Structures in Ionic Solids
We've learned a lot about covalent compounds, but we haven't talked quite as much about ionic compounds in their solid state. These will adopt a highly ordered and repeating lattice structure, but the geometry of the lattice depends entirely on the types of ions and their ratio in the chem
From playlist General Chemistry

Lattice relations + Hermite normal form|Abstract Algebra Math Foundations 224 | NJ Wildberger
We introduce lattices and integral linear spans of vexels. These are remarkably flexible, common and useful algebraic objects, and they are the direct integral analogs of vector spaces. To understand the structure of a given lattice, the algorithm to compute a Hermite normal form basis is
From playlist Math Foundations

Mod-01 Lec-5ex Diffraction Methods For Crystal Structures - Worked Examples
Condensed Matter Physics by Prof. G. Rangarajan, Department of Physics, IIT Madras. For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist NPTEL: Condensed Matter Physics - CosmoLearning.com Physics Course

MF150: What exactly is a set? | Data Structures in Mathematics Math Foundations | NJ Wildberger
What exactly is a set?? This is a crucial question in the modern foundations of mathematics. Here we begin an examination of this thorny issue, first by discussing the usual English usage of the term, as well as alternate terms, such as collection, aggregate, bunch, class, menagerie etc th
From playlist Math Foundations

From playlist Exploratory Data Analysis

Now that we know what a quotient group is, let's take a look at an example to cement our understanding of the concepts involved.
From playlist Abstract algebra

Dihedral Group (Abstract Algebra)
The Dihedral Group is a classic finite group from abstract algebra. It is a non abelian groups (non commutative), and it is the group of symmetries of a regular polygon. This group is easy to work with computationally, and provides a great example of one connection between groups and geo
From playlist Abstract Algebra

This is a historical talk giving my recollections of how vertex algebras were discovered. It was requested by Michael Penn for his series of videos on vertex algebras https://www.youtube.com/playlist?list=PL22w63XsKjqyx2FFUywi_mz91Jtih52yX
From playlist Math talks

The Genesis of Vertex Algebras
We have a guest for this very special video. Richard Borcherds (Berkeley) has contributed a video regarding the history of vertex algebras. This video was also posted on his channel and is included here as well with permission and to increase its reach. Subscribe to his channel: https:/
From playlist Vertex Operator Algebras

Tathagata Basak: A monstrous(?) complex hyperbolic orbifold
I will report on progress with Daniel Allcock on the ”Monstrous Proposal”, namely the conjecture: Complex hyperbolic 13-space, modulo a particular discrete group, and with orbifold structure changed in a simple way, has fundamental group equal to (MxM)(semidirect)2, where M is the Monster
From playlist Topology

Modular forms: Theta functions in higher dimensions
This lecture is part of an online graduate course on modular forms. We study theta functions of even unimodular lattices, such as the root lattice of the E8 exceptional Lie algebra. As examples we show that one cannot "her the shape of a drum", and calculate the number of minimal vectors
From playlist Modular forms

Sphere packings in 8 dimensions (after Maryna Viazovska)
The is a math talk about the best possible sphere packing in 8 dimensions. It was an open problem for many years to show that the best 8-dimensional sphere packing is given by the E8 lattice. We describe the solution to this found by Maryna Viazovska, building on work of Henry Cohn and Noa
From playlist Math talks

This is an informal talk on sporadic groups given to the Archimedeans (the Cambridge undergraduate mathematical society). It discusses the classification of finite simple groups and some of the sporadic groups, and finishes by briefly describing monstrous moonshine. For other Archimedeans
From playlist Math talks

Moonshine - 2 by Suresh Govindarajan
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Isometry groups of the projective line (I) | Rational Geometry Math Foundations 138 | NJ Wildberger
The projective line can be given a Euclidean structure, just as the affine line can, but it is a bit more complicated. The algebraic structure of this projective line supports some symmetries. Symmetry in mathematics is often most efficiently encoded with the idea of a group--a technical t
From playlist Math Foundations
