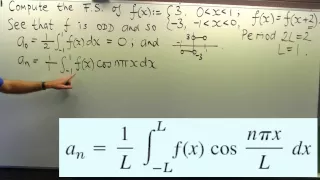Fourier series
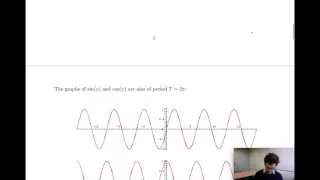
A Fourier series (/ˈfʊrieɪ, -iər/) is a summation of harmonically related sinusoidal functions, also known as components or harmonics. The result of the summation is a periodic function whose functional form is determined by the choices of cycle length (or period), the number of components, and their amplitudes and phase parameters. With appropriate choices, one cycle (or period) of the summation can be made to approximate an arbitrary function in that interval (or the entire function if it too is periodic). The number of components is theoretically infinite, in which case the other parameters can be chosen to cause the series to converge to almost any well behaved periodic function (see Pathological and Dirichlet conditions). The components of a particular function are determined by analysis techniques described in this article. Sometimes the components are known first, and the unknown function is synthesizedby a Fourier series. Such is the case of a discrete-time Fourier transform. Convergence of Fourier series means that as more and more components from the series are summed, each successive partial Fourier series sum will better approximate the function, and will equal the function with a potentially infinite number of components. The mathematical proofs for this may be collectively referred to as the Fourier Theorem (see ). The figures below illustrate some partial Fourier series results for the components of a square wave. * A square wave (represented as the blue dot) is approximated by its sixth partial sum (represented as the purple dot), formed by summing the first six terms (represented as arrows) of the square wave's Fourier series. Each arrow starts at the vertical sum of all the arrows to its left (i.e. the previous partial sum). * The first four partial sums of the Fourier series for a square wave. As more harmonics are added, the partial sums converge to (become more and more like) the square wave. * Function (in red) is a Fourier series sum of 6 harmonically related sine waves (in blue). Its Fourier transform is a frequency-domain representation that reveals the amplitudes of the summed sine waves. Another analysis technique (not covered here), suitable for both periodic and non-periodic functions, is the Fourier transform, which provides a frequency-continuum of component information. But when applied to a periodic function all components have zero amplitude, except at the harmonic frequencies. The inverse Fourier transform is a synthesis process (like the Fourier series), which converts the component information (often known as the frequency domain representation) back into its time domain representation. Since Fourier's time, many different approaches to defining and understanding the concept of Fourier series have been discovered, all of which are consistent with one another, but each of which emphasizes different aspects of the topic. Some of the more powerful and elegant approaches are based on mathematical ideas and tools that were not available in Fourier's time. Fourier originally defined the Fourier series for real-valued functions of real arguments, and used the sine and cosine functions as the basis set for the decomposition. Many other Fourier-related transforms have since been defined, extending his initial idea to many applications and birthing an area of mathematics called Fourier analysis. (Wikipedia).