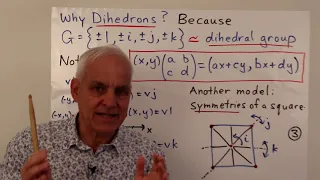Historical treatment of quaternions
History of quaternions
In mathematics, quaternions are a non-commutative number system that extends the complex numbers. Quaternions and their applications to rotations were first described in print by Olinde Rodrigues in all but name in 1840, but independently discovered by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. They find uses in both theoretical and applied mathematics, in particular for calculations involving three-dimensional rotations. (Wikipedia).
_regarding_the_discovery_of_Quaternions_multiplication_by_Sir_William_Rowan_Hamilton.jpg?width=300)