
Continued Fraction Expansions, Pt. III
A fascinating generalization linking sequences, continued fractions, and polynomials. Email: allLogarithmsWereCreatedEqual@gmail.com Subscribe! https://www.youtube.com/AllLogarithmsEqual
From playlist Number Theory

The first part develops the fraction from a simple equation or statement with a single unknown variable and demonstrates the recursive, iterative procedure. Possibly as simple and straightforward as it is possible for me to do. The second part still confuses me and amounts to no mare than
From playlist Number Theory

This video defines what a simplified fraction is and explains how to simplify fractions using prime factors and division.
From playlist Simplifying Fractions

Arithmetic With... Continued Fractions?? #SoME2
Arithmetic! On continued fractions! It's possible, but not well known or widely used in practice. This video explores the basics of this underappreciated area of math. This is my submission for SoME2 (https://www.youtube.com/watch?v=hZuYICAEN9Y&t=0s) SOURCES & FURTHER READING: Continued
From playlist Summer of Math Exposition 2 videos

Infinite Continued Fractions, simple or not?
Start learning today, click https://brilliant.org/blackpenredpen/ to check out Brillant.org. First 200 people to sign up will get 20% off your annual premium subscription! What Are Continued Fractions? Continued Fractions, Write sqrt(2) as a continued fraction, infinite simple continued
From playlist [Math For Fun] Brilliant Problems
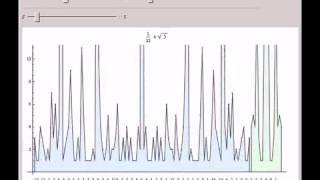
Graphing Continued Fractions of Quadratic Irrationals
http://demonstrations.wolfram.com/GraphingContinuedFractionsOfQuadraticIrrationals The Wolfram Demonstrations Project contains thousands of free interactive visualizations, with new entries added daily. Let x= ( a ) / ( b ) + ( c ) / ( d ) SqrtBox[S], a,b,c,d,S??. The continued fraction
From playlist Number Theory

Keith Conrad (University of Connecticut) — January 28, 2015
From playlist Number Theory

Continued Fraction Expansions Part II: Example Calculations
Complete with calculations and exercises! Let me know what you come up with. NEW (2016 Season): See Episode 3 here! https://youtu.be/4U9z5qoiDNQ ----- Sources for additional information: Very useful informative article (no surprise, it's from MathWorld): http://mathworld.wolfram.com/Con
From playlist Number Theory

2023 Number Challenge: Rational Approximation for Square Root 2023
In this video, we look at how to use continued fraction to approximate square root of 2023, which is an irrational number. sqrt(2023) ≈ 44.9777722277722277 It can be approximated by two forms of continued fraction: 44 + 88/ (87 + 88/ (87 + 88/ (87 .... )))) Or in a simple continued fr
From playlist Math Problems with Number 2023
Jörg Thuswaldner: Multidimensional continued fractions and symbolic codings of toral translations
CIRM VIRTUAL CONFERENCE Recorded during the meeting " Diophantine Problems, Determinism and Randomness" the November 24, 2020 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide
From playlist Virtual Conference

Mathematical Games Hosted by Ed Pegg Jr. [Episode 2: Fun with Fractions]
Join Ed Pegg Jr. as he explores a variety of games and puzzles using Wolfram Language. In this episode, he features games and puzzles using fractions. Follow us on our official social media channels. Twitter: https://twitter.com/WolframResearch/ Facebook: https://www.facebook.com/wo
From playlist Mathematical Games Hosted by Ed Pegg Jr.

Laura Capuano: An effective criterion for periodicity of p-adic continued fractions
Abstract: It goes back to Lagrange that a real quadratic irrational has always a periodic continued fraction. Starting from decades ago, several authors proposed different definitions of a p-adic continued fraction, and the definition depends on the chosen system of residues mod p. It turn
From playlist Women at CIRM

Gronwall's inequality & fractional differential equations
Several general versions of Gronwall's inequality are presented and applied to fractional differential equations of arbitrary order. Applications include: yielding a priori bounds and nonumultiplicity of solutions. This presentation features new mathematical research. http://projecteucli
From playlist Mathematical analysis and applications
Jörg Thuswaldner: S-adic sequences: a bridge between dynamics, arithmetic, and geometry
Abstract: Based on work done by Morse and Hedlund (1940) it was observed by Arnoux and Rauzy (1991) that the classical continued fraction algorithm provides a surprising link between arithmetic and diophantine properties of an irrational number αα, the rotation by αα on the torus 𝕋=ℝ/ℤT=R/
From playlist Dynamical Systems and Ordinary Differential Equations

Giuseppe Mingione - 23 September 2016
Mingione, Giuseppe "Recent progresses in nonlinear potential theory"
From playlist A Mathematical Tribute to Ennio De Giorgi

Infinite fractions and the most irrational number
NEW: Follow-up video with puzzle solution is here: https://youtu.be/leFep9yt3JY In this video the Mathologer uses infinite fractions to track down the most irrational of all irrational numbers. Find out about how the usual suspects root 2, e, and pi stack up against this special number and
From playlist Recent videos