
Abstract Algebra | Normal Subgroups
We give the definition of a normal subgroup and give some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra
The Normal Distribution (1 of 3: Introductory definition)
More resources available at www.misterwootube.com
From playlist The Normal Distribution

Before we carry on with our coset journey, we need to discover when the left- and right cosets are equal to each other. The obvious situation is when our group is Abelian. The other situation is when the subgroup is a normal subgroup. In this video I show you what a normal subgroup is a
From playlist Abstract algebra

We are – almost all of us – deeply attracted to the idea of being normal. But what if our idea of ‘normal’ isn’t normal? A plea for a broader definition of an important term. If you like our films, take a look at our shop (we ship worldwide): https://goo.gl/ojRR53 Join our mailing list: h
From playlist SELF
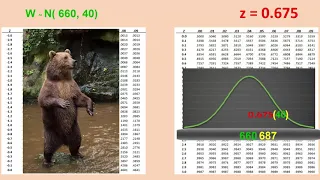
Determining values of a variable at a particular percentile in a normal distribution
From playlist Unit 2: Normal Distributions

Direct Product of Normal Subgroups is Normal Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Direct Product of Normal Subgroups is Normal Proof. In this video we prove that if A is a normal subgroup of G and B is a normal subgroup of H, then A x B is a normal subgroup of G x H.
From playlist Abstract Algebra

Normal Subgroups and Quotient Groups (aka Factor Groups) - Abstract Algebra
Normal subgroups are a powerful tool for creating factor groups (also called quotient groups). In this video we introduce the concept of a coset, talk about which subgroups are “normal” subgroups, and show when the collection of cosets can be treated as a group of their own. As a motivat
From playlist Abstract Algebra

More Standard Deviation and Variance
Further explanations and examples of standard deviation and variance
From playlist Unit 1: Descriptive Statistics

Difference Between Normalizer, Centralizer, and Stabilizer
An easy way to remember what is the normalizer and centralizer of a subgroup, and what is the stabilizer of an element under a group action. For people learning abstract algebra! Group Theory playlist: https://youtube.com/playlist?list=PLug5ZIRrShJHDvvls4OtoBHi6cNnTZ6a6 Subscribe to see
From playlist Group Theory

Lie Groups and Lie Algebras: Lesson 43 Group Theory Review #2 (improved video quality)
Lie Groups and Lie Algebras: Lesson 43 Group Theory Review #2 In this lecture we examine a great way of becoming familiar with the smaller groups: the subgroup lattice. We use this to remind ourselves about normal subgroups, cyclic subgroups, and the center of a group. Errata!: The norma
From playlist Lie Groups and Lie Algebras

Lie Groups and Lie Algebras: Lesson 44 Group Theory Review #3 (corrected!)
Lie Groups and Lie Algebras: Lesson 44 Group Theory Review #3 This is a corrected version of a previous upload. In the earlier version I ridiculously stated that cyclic subgroups were normal. I don't know what came over me, that is certainly NOT true. What is true is that if a group is a
From playlist Lie Groups and Lie Algebras

Visual Group Theory, Lecture 4.5: The isomorphism theorems
Visual Group Theory, Lecture 4.5: The isomorphism theorems There are four central results in group theory that are collectively known at the isomorphism theorems. We introduced the first of these a few lectures back, under the name of the "fundamental homomorphism theorem." In this lectur
From playlist Visual Group Theory

Visual Group Theory, Lecture 5.3: Examples of group actions
Visual Group Theory, Lecture 5.3: Examples of group actions It is frequently of interest to analyze the action of a group on its elements (by multiplication), subgroups (by multiplication, or by conjugation), or cosets (by multiplication). We look at all of these, and analyze the orbits,
From playlist Visual Group Theory

No simple groups of order 66 or 144.
We look at an "advanced" group theory problem that uses Sylow's Theorems to show that there are no simple groups of order 66 or 144. Suggest a problem: https://forms.gle/ea7Pw7HcKePGB4my5 Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Merch: https://teespri
From playlist Assorted Group Theory

Abstract Algebra - 9.1 Normal Subgroups
We begin Chapter 9 by looking closely at something called a Normal Subgroup. Our study to begin chapter 9 is essential to understanding factor groups in our next video. We also revisit the idea of conjugation, which we brought up previously but didn't give a name to. Video Chapters: Intro
From playlist Abstract Algebra - Entire Course
Abstract Algebra class April 13, 2021
Suggest a problem: https://forms.gle/ea7Pw7HcKePGB4my5 Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Merch: https://teespring.com/stores/michael-penn-math Personal Website: http://www.michael-penn.net Randolph College Math: http://www.randolphcollege.edu/ma
From playlist Super Lo-fi in class videos

Visual Group Theory, Lecture 3.6: Normalizers
Visual Group Theory, Lecture 3.6: Normalizers A subgroup H of G is normal if xH=Hx for all x in G. If H is not normal, then the normalizer is the set of elements for which xH=Hx. Obviously, the normalizer has to be at least H and at most G, and so in some sense, this is measuring "how clo
From playlist Visual Group Theory

Group theory 6: normal subgroups and quotient groups
This is lecture 6 of an online mathematics course on groups theory. It defines normal subgroups and quotient groups, using the non-abelian group of order 6 as an example.
From playlist Group theory

Visual Group Theory, Lecture 3.3: Normal subgroups
Visual Group Theory, Lecture 3.3: Normal subgroups A subgroup H of G is normal if every left coset gH equals the right coset Hg. In this lecture, we see several different ways of visualizing this concept as well as several equivalent definitions. We conclude with three useful but differen
From playlist Visual Group Theory

Group Theory: The Simple Group of Order 168 - Part 1
We present two realizations of the simple group of order 168. In part 1, we count the number of matrices in PSL(2,Z/7) and SL(3,Z/2).
From playlist *** The Good Stuff ***