
Abstract Algebra | Normal Subgroups
We give the definition of a normal subgroup and give some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Before we carry on with our coset journey, we need to discover when the left- and right cosets are equal to each other. The obvious situation is when our group is Abelian. The other situation is when the subgroup is a normal subgroup. In this video I show you what a normal subgroup is a
From playlist Abstract algebra

In this tutorial we define a subgroup and prove two theorem that help us identify a subgroup. These proofs are simple to understand. There are also two examples of subgroups.
From playlist Abstract algebra

Abstract Algebra | The notion of a subgroup.
We present the definition of a subgroup and give some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra
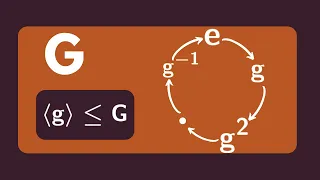
Abstract Algebra | Cyclic Subgroups
We define the notion of a cyclic subgroup and give a few examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Definition of a Subgroup in Abstract Algebra with Examples of Subgroups
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Subgroup in Abstract Algebra with Examples of Subgroups
From playlist Abstract Algebra

Jordan Sahattchieve: A Fibering Theorem for 3-Manifolds
Jordan Sahattchieve Title: A Fibering Theorem for 3-Manifolds In this talk, I will endeavor to communicate a new fibering theorem for 3-manifolds in the style of Stalling's Fibration Theorem.
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

D. Vittone - Rectifiability issues in sub-Riemannian geometry
In this talk we discuss two problems concerning “rectifiability” in sub-Riemannian geometry and particularly in the model setting of Carnot groups. The first problem regards the rectifiability of boundaries of sets with finite perimeter in Carnot groups, while the second one concerns Radem
From playlist Journées Sous-Riemanniennes 2018

Latha Palaniappan, Stanford University: Big Data in Biomedicine Conference
Bringing together thought leaders in large-scale data analysis and technology to transform the way we diagnose, treat and prevent disease. Learn more: http://stanford.io/1M8v9ra
From playlist Big Data in Biomedicine Conference 2015
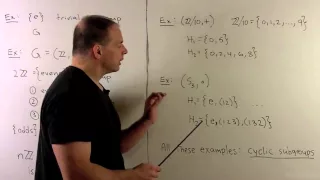
Abstract Algebra: We define the notion of a subgroup and provide various examples. We also consider cyclic subgroups and subgroups generated by subsets in a given group G. Example include A4 and D8. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-
From playlist Abstract Algebra

Jennifer Johnston, MA, LPC, “Neurobiology of Suicidality: A View from Neuroimaging”
Jennifer Johnston, MA, LPC is a researcher at Yale and clinician in private practice with expertise in emotion regulation difficulties and suicidal behaviors in youths and adults. She completed her master’s degree in Mental Health Counseling and Behavioral Medicine at Boston University Sch
From playlist 12th Annual Yale NEA-BPD Conference

Normal subgroups and quotient groups
Jacob explains how homomorphisms and their kernels give rise to quotient groups, and sketches a proof of the First Isomorphism Theorem, a useful result in group theory.
From playlist Basics: Group Theory

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra
J. Bruinier et J. Ignacio Burgos Gil - Arakelov theory on Shimura varieties (part1)
A Shimura variety is a higher-dimensional analogue of a modular curve that arises as a quotient of a Hermitian symmetric space by a congruence subgroup of a reductive algebraic group defined over Q. Shimura varieties have a very rich geometric and arithmetic structure. For instance they ar
From playlist Ecole d'été 2017 - Géométrie d'Arakelov et applications diophantiennes
21. Automating Clinical Work Flows
MIT 6.S897 Machine Learning for Healthcare, Spring 2019 Instructor: Peter Szolovits View the complete course: https://ocw.mit.edu/6-S897S19 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP60B0PQXVQyGNdCyCTDU1Q5j Prof. Szolovits discusses ways of improving medical care a
From playlist MIT 6.S897 Machine Learning for Healthcare, Spring 2019

An general explanation of the underactive thyroid.
From playlist For Patients

Frontiers of AI in Medical Imaging for Clinical Decision Making
From the November 1st, 2017 Human AI Collaboration: A Dynamic Frontier Conference; Daniel Rubin, Associate Professor of Biomedical Data Science, Radiology, Medicine (Biomedical Informatics Research), and Ophthalmology (courtesy), Stanford University looks at... 1. There is much variabilit
From playlist Human AI Collaboration: A Dynamic Frontier Conference

Alexander Olshanskii - Relative growth of subgroups in finitely generated groups
Alexander Olshanskii (Vanderbilt University, USA and Moscow State University, Russia) Let $H$ be a subgroup of a finitely generated group $G$. The (relative) growth function $f(n)$ of $H$ with respect to a finite set $A$ generating $G$, is given by the formula $f(n) = card \{g\in H;
From playlist T1-2014 : Random walks and asymptopic geometry of groups.

A group is (in a sense) the simplest structure in which we can do the familiar tasks associated with "algebra." First, in this video, we review the definition of a group.
From playlist Modern Algebra - Chapter 15 (groups)
