
Definition of a Subgroup in Abstract Algebra with Examples of Subgroups
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Subgroup in Abstract Algebra with Examples of Subgroups
From playlist Abstract Algebra

In this tutorial we define a subgroup and prove two theorem that help us identify a subgroup. These proofs are simple to understand. There are also two examples of subgroups.
From playlist Abstract algebra
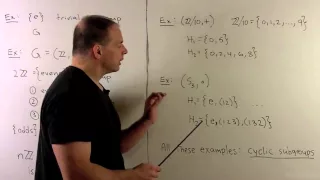
Abstract Algebra: We define the notion of a subgroup and provide various examples. We also consider cyclic subgroups and subgroups generated by subsets in a given group G. Example include A4 and D8. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-
From playlist Abstract Algebra

Abstract Algebra | Normal Subgroups
We give the definition of a normal subgroup and give some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Modern Algebra - Chapter 18: Subgroups
Redfield Chapter 18: Subgroups
From playlist Modern Algebra - Chapter 18

Jordan Sahattchieve: A Fibering Theorem for 3-Manifolds
Jordan Sahattchieve Title: A Fibering Theorem for 3-Manifolds In this talk, I will endeavor to communicate a new fibering theorem for 3-manifolds in the style of Stalling's Fibration Theorem.
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022
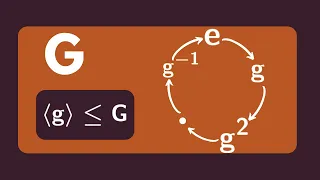
Abstract Algebra | Cyclic Subgroups
We define the notion of a cyclic subgroup and give a few examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

A group is (in a sense) the simplest structure in which we can do the familiar tasks associated with "algebra." First, in this video, we review the definition of a group.
From playlist Modern Algebra - Chapter 15 (groups)

Bettina EICK - Computational group theory, cohomology of groups and topological methods 1
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to use them within GAP. Alexander Hulpke's lectures will being with some general computation
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Alexander HULPKE - Computational group theory, cohomology of groups and topological methods 3
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to use them within GAP. Alexander Hulpke's lectures will being with some general computation
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

GT23. Composition and Classification
Abstract Algebra: We use composition series as another technique for studying finite groups, which leads to the notion of solvable groups and puts the focus on simple groups. From there, we survey the classification of finite simple groups and the Monster group.
From playlist Abstract Algebra

Abstract Algebra | The notion of a subgroup.
We present the definition of a subgroup and give some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Group theory 29:The Jordan Holder theorem
This lecture is part of an online course on group theory. It covers the Jordan-Holder theorem, staring that the simple groups appearing in a composition series of a finite group do not depend on the composition series.
From playlist Group theory

The Special Linear Group is a Subgroup of the General Linear Group Proof
The Special Linear Group is a Subgroup of the General Linear Group Proof
From playlist Abstract Algebra

Metric Spaces - Lectures 13 & 14: Oxford Mathematics 2nd Year Student Lecture
For the first time we are making a full Oxford Mathematics Undergraduate lecture course available. Ben Green's 2nd Year Metric Spaces course is the first half of the Metric Spaces and Complex Analysis course. This is the 7th of 11 videos. The course is about the notion of distance. You ma
From playlist Oxford Mathematics Student Lectures - Metric Spaces

Bettina EICK - Computational group theory, cohomology of groups and topological methods 5
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to use them within GAP. Alexander Hulpke's lectures will being with some general computation
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

On characterization of monomial irreducible representations by Pooja Singla
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Units in a Ring (Abstract Algebra)
The units in a ring are those elements which have an inverse under multiplication. They form a group, and this “group of units” is very important in algebraic number theory. Using units you can also define the idea of an “associate” which lets you generalize the fundamental theorem of ar
From playlist Abstract Algebra

Tongmu He: Sen operators and Lie algebras arising from Galois representations over p-adic varieties
HYBRID EVENT Recorded during the meeting "Franco-Asian Summer School on Arithmetic Geometry in Luminy" the June 03, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Luca Recanzone Find this video and other talks given by worldwide mathematicia
From playlist Algebraic and Complex Geometry
