
Abstract Algebra | Normal Subgroups
We give the definition of a normal subgroup and give some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra
From playlist everything

In this tutorial we define a subgroup and prove two theorem that help us identify a subgroup. These proofs are simple to understand. There are also two examples of subgroups.
From playlist Abstract algebra

Group Definition (expanded) - Abstract Algebra
The group is the most fundamental object you will study in abstract algebra. Groups generalize a wide variety of mathematical sets: the integers, symmetries of shapes, modular arithmetic, NxM matrices, and much more. After learning about groups in detail, you will then be ready to contin
From playlist Abstract Algebra

Definition of a Subgroup in Abstract Algebra with Examples of Subgroups
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Subgroup in Abstract Algebra with Examples of Subgroups
From playlist Abstract Algebra

A group is (in a sense) the simplest structure in which we can do the familiar tasks associated with "algebra." First, in this video, we review the definition of a group.
From playlist Modern Algebra - Chapter 15 (groups)
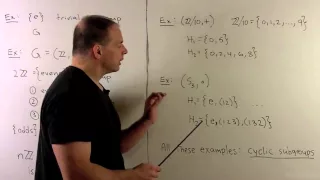
Abstract Algebra: We define the notion of a subgroup and provide various examples. We also consider cyclic subgroups and subgroups generated by subsets in a given group G. Example include A4 and D8. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-
From playlist Abstract Algebra
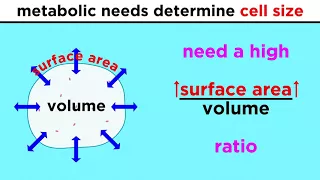
Prokaryotic Cells: The Simplest Kind of Life
We've established that the basic unit of life is the cell, and that the simplest forms of life are just one cell. The earliest unicellular organisms were prokaryotic, and there are many prokaryotic organisms still around today, including all bacteria. So let's go over the features of the p
From playlist Biology/Genetics

Karen Vogtmann - On the cohomological dimension of automorphism groups of RAAGs
The class of right-angled Artin groups (RAAGs) includes free groups and free abelian groups, Both of these have extremely interesting automorphism groups, which share some properties and not others. We are interested in automorphism groups of general RAAGs, and in particular
From playlist Groupes, géométrie et analyse : conférence en l'honneur des 60 ans d'Alain Valette

Lie Groups and Lie Algebras: Lesson 43 Group Theory Review #2 (improved video quality)
Lie Groups and Lie Algebras: Lesson 43 Group Theory Review #2 In this lecture we examine a great way of becoming familiar with the smaller groups: the subgroup lattice. We use this to remind ourselves about normal subgroups, cyclic subgroups, and the center of a group. Errata!: The norma
From playlist Lie Groups and Lie Algebras

Cyclic Groups -- Abstract Algebra 7
⭐Support the channel⭐ Patreon: https://www.patreon.com/michaelpennmath Merch: https://teespring.com/stores/michael-penn-math My amazon shop: https://www.amazon.com/shop/michaelpenn 🟢 Discord: https://discord.gg/Ta6PTGtKBm ⭐my other channels⭐ Main Channel: https://www.youtube.
From playlist Abstract Algebra

Lie Groups and Lie Algebras: Lesson 44 Group Theory Review #3 (corrected!)
Lie Groups and Lie Algebras: Lesson 44 Group Theory Review #3 This is a corrected version of a previous upload. In the earlier version I ridiculously stated that cyclic subgroups were normal. I don't know what came over me, that is certainly NOT true. What is true is that if a group is a
From playlist Lie Groups and Lie Algebras

Lagrange's Theorem and Index of Subgroups | Abstract Algebra
We introduce Lagrange's theorem, showing why it is true and follows from previously proven results about cosets. We also investigate groups of prime order, seeing how Lagrange's theorem informs us about every group of prime order - in particular it tells us that any group of prime order p
From playlist Abstract Algebra

Visual Group Theory, Lecture 4.5: The isomorphism theorems
Visual Group Theory, Lecture 4.5: The isomorphism theorems There are four central results in group theory that are collectively known at the isomorphism theorems. We introduced the first of these a few lectures back, under the name of the "fundamental homomorphism theorem." In this lectur
From playlist Visual Group Theory

Visual Group Theory, Lecture 5.3: Examples of group actions
Visual Group Theory, Lecture 5.3: Examples of group actions It is frequently of interest to analyze the action of a group on its elements (by multiplication), subgroups (by multiplication, or by conjugation), or cosets (by multiplication). We look at all of these, and analyze the orbits,
From playlist Visual Group Theory

Group theory 15:Groups of order 12
This lecture is part of an online mathematics course on group theory. It uses the Sylow theorems to classify the groups of order 12, and finds their subgroups.
From playlist Group theory

No simple groups of order 66 or 144.
We look at an "advanced" group theory problem that uses Sylow's Theorems to show that there are no simple groups of order 66 or 144. Suggest a problem: https://forms.gle/ea7Pw7HcKePGB4my5 Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Merch: https://teespri
From playlist Assorted Group Theory

Why Normal Subgroups are Necessary for Quotient Groups
Proof that cosets are disjoint: https://youtu.be/uxhAUmgSHnI In order for a subgroup to create a quotient group (also known as factor group), it must be a normal subgroup. That means that when we conjugate an element in the subgroup, it stays in the subgroup. In this video, we explain wh
From playlist Group Theory

Visual Group Theory, Lecture 3.1: Subgroups
Visual Group Theory, Lecture 3.1: Subgroups In this lecture, we begin by examining a property about Cayley graphs called "regularity" that we've hinted at but not yet spelled out explicitly. Next, we introduce the concept of a subgroup, provide some examples, and show how the subgroups of
From playlist Visual Group Theory

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra