
Group Theory: The Center of a Group G is a Subgroup of G Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Group Theory: The Center of a Group G is a Subgroup of G Proof
From playlist Abstract Algebra

Symmetric Groups (Abstract Algebra)
Symmetric groups are some of the most essential types of finite groups. A symmetric group is the group of permutations on a set. The group of permutations on a set of n-elements is denoted S_n. Symmetric groups capture the history of abstract algebra, provide a wide range of examples in
From playlist Abstract Algebra

The Special Linear Group is a Subgroup of the General Linear Group Proof
The Special Linear Group is a Subgroup of the General Linear Group Proof
From playlist Abstract Algebra
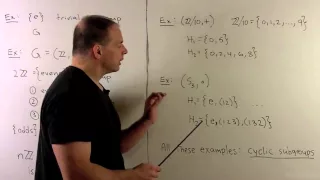
Abstract Algebra: We define the notion of a subgroup and provide various examples. We also consider cyclic subgroups and subgroups generated by subsets in a given group G. Example include A4 and D8. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-
From playlist Abstract Algebra
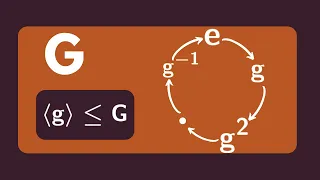
Abstract Algebra | Cyclic Subgroups
We define the notion of a cyclic subgroup and give a few examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

What is a Group? | Abstract Algebra
Welcome to group theory! In today's lesson we'll be going over the definition of a group. We'll see the four group axioms in action with some examples, and some non-examples as well which violate the axioms and are thus not groups. In a fundamental way, groups are structures built from s
From playlist Abstract Algebra

Group Definition (expanded) - Abstract Algebra
The group is the most fundamental object you will study in abstract algebra. Groups generalize a wide variety of mathematical sets: the integers, symmetries of shapes, modular arithmetic, NxM matrices, and much more. After learning about groups in detail, you will then be ready to contin
From playlist Abstract Algebra

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

Now that we know what a quotient group is, let's take a look at an example to cement our understanding of the concepts involved.
From playlist Abstract algebra
Examples of non-positively curved groups II - Kim Ruane
Women and Mathematics Title: Examples of non-positively curved groups II Speaker: Kim Ruane Affiliation: Tufts University Date: May 24, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Colloquium MathAlp 2019 - Claude Lebrun
Claude Lebrun - Mass, Scalar Curvature, Kähler Geometry, and All That Given a complete Riemannian manifold that looks enough like Euclidean space at infinity, physicists have defined a quantity called the “mass” that measures the asymptotic deviation of the geometry from the Euclidean mod
From playlist Colloquiums MathAlp

Dynamics on character varieties - William Goldman
Character Varieties, Dynamics and Arithmetic Topic: Dynamics on character varieties Speaker: William Goldman Affiliation: University of Maryland; Member, School of Mathematics Date: November 10, 2021 In these two talks, I will describe how the classification of locally homogeneous geomet
From playlist Mathematics

Intrinsic Diophantine approximation (Lecture 1) by Amos Nevo
PROGRAM SMOOTH AND HOMOGENEOUS DYNAMICS ORGANIZERS: Anish Ghosh, Stefano Luzzatto and Marcelo Viana DATE: 23 September 2019 to 04 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Ergodic theory has its origins in the the work of L. Boltzmann on the kinetic theory of gases.
From playlist Smooth And Homogeneous Dynamics

Week 7 - Symmetry and Equivariance in Neural Networks - Tess Smidt
More about this lecture: https://dl4sci-school.lbl.gov/tess-smidt Deep Learning for Science School: https://dl4sci-school.lbl.gov/agenda
From playlist ML & Deep Learning

Visual Group Theory: Lecture 7.5: Euclidean domains and algebraic integers
Visual Group Theory: Lecture 7.5: Euclidean domains and algebraic integers. Around 300 BC, the Greek mathematician Euclid found an algorithm to compute the greatest common divisor (gcd) of two numbers. Loosely speaking, a Euclidean domain is a commutative ring for which this algorihm stil
From playlist Visual Group Theory

This lecture was held by Abel Laureate John Milnor at The University of Oslo, May 25, 2011 and was part of the Abel Prize Lectures in connection with the Abel Prize Week celebrations. Program for the Abel Lectures 2011 1. "Spheres" by Abel Laureate John Milnor, Institute for Mathematical
From playlist Abel Lectures

Prerequisites III: Manifolds & Fiber Bundles - Maurice Weiler
Video recording of the First Italian Summer School on Geometric Deep Learning, which took place in July 2022 in Pescara. Slides: https://www.sci.unich.it/geodeep2022/slides/Manifolds_and_Fiber_Bundles.pdf
From playlist First Italian School on Geometric Deep Learning - Pescara 2022

Abstract Algebra | The notion of a subgroup.
We present the definition of a subgroup and give some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Nov. 17, Chapter 18 (Semi-direct products)
From playlist Fall 2020 Course
