
Inner & Outer Semidirect Products Derivation - Group Theory
Semidirect products are a very important tool for studying groups because they allow us to break a group into smaller components using normal subgroups and complements! Here we describe a derivation for the idea of semidirect products and an explanation of how the map into the automorphism
From playlist Group Theory

Walter van Suijlekom: Semigroup of inner perturbations in Non Commutative Geometry
Starting with an algebra, we define a semigroup which extends the group of invertible elements in that algebra. As we will explain, this semigroup describes inner perturbations of noncommutative manifolds, and has applications to gauge theories in physics. We will present some elementary e
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

In this tutorial we define a subgroup and prove two theorem that help us identify a subgroup. These proofs are simple to understand. There are also two examples of subgroups.
From playlist Abstract algebra
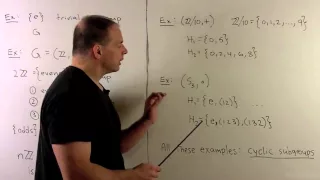
Abstract Algebra: We define the notion of a subgroup and provide various examples. We also consider cyclic subgroups and subgroups generated by subsets in a given group G. Example include A4 and D8. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-
From playlist Abstract Algebra

Definition of a Subgroup in Abstract Algebra with Examples of Subgroups
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Subgroup in Abstract Algebra with Examples of Subgroups
From playlist Abstract Algebra

Group theory 7: Semidirect products
This is lecture 7 of an online course on group theory. It covers semidirect products and uses them to classify groups of order 6.
From playlist Group theory

Darij Grinberg - The one-sided cycle shuffles in the symmetric group algebra
We study a new family of elements in the group ring of a symmetric group – or, equivalently, a class of ways to shuffle a deck of cards. Fix a positive integer n. Consider the symmetric group S_n. For each 1 ≤ ℓ ≤ n, we define an element t_ℓ := cyc_ℓ + cyc{ℓ,ℓ+1} + cyc_{ℓ,ℓ+1,ℓ+2} + · · ·
From playlist Combinatorics and Arithmetic for Physics: Special Days 2022

"Concatenation theorems for the Gowers uniformity norms, and applications" Terence Tao [2015]
Terence Tao, University of California, Los Angeles Concatenation theorems for the Gowers uniformity norms, and applications Abstract: Abstract: A function P(n, m) of two variables which is a polynomial of degree less than d1 in the n variable, and a polynomial of degree less than d2 in th
From playlist Mathematics

Lecture 3: Quotient Spaces, the Baire Category Theorem and the Uniform Boundedness Theorem
MIT 18.102 Introduction to Functional Analysis, Spring 2021 Instructor: Dr. Casey Rodriguez View the complete course: https://ocw.mit.edu/courses/18-102-introduction-to-functional-analysis-spring-2021/ YouTube Playlist: https://www.youtube.com/watch?v=58B5dEJReQ8&list=PLUl4u3cNGP63micsJp_
From playlist MIT 18.102 Introduction to Functional Analysis, Spring 2021

Before we carry on with our coset journey, we need to discover when the left- and right cosets are equal to each other. The obvious situation is when our group is Abelian. The other situation is when the subgroup is a normal subgroup. In this video I show you what a normal subgroup is a
From playlist Abstract algebra
Martin Schweizer: Some stochastic Fubini theorems
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Analysis and its Applications

Semi-coarse Spaces, Homotopy [Jonathan Treviño-Marroquín]
Semi-coarse spaces is an alternative to study (undirected) graphs through large-scale geometry. In this video, we present the structure and a homotopy what we worked on. In the final part, we look at the fundamental homotopy group of cyclic graphs.
From playlist Contributed Videos
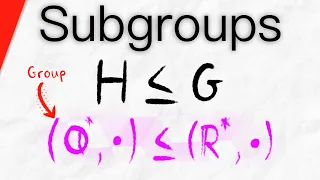
All About Subgroups | Abstract Algebra
We introduce subgroups, the definition of subgroup, examples and non-examples of subgroups, and we prove that subgroups are groups. We also do an example proving a subset is a subgroup. If G is a group and H is a nonempty subset of G, we say H is a subgroup of G if H is closed with respect
From playlist Abstract Algebra

Lie Groups and Lie Algebras: Lesson 43 Group Theory Review #2 (improved video quality)
Lie Groups and Lie Algebras: Lesson 43 Group Theory Review #2 In this lecture we examine a great way of becoming familiar with the smaller groups: the subgroup lattice. We use this to remind ourselves about normal subgroups, cyclic subgroups, and the center of a group. Errata!: The norma
From playlist Lie Groups and Lie Algebras

Cyclic Groups -- Abstract Algebra 7
⭐Support the channel⭐ Patreon: https://www.patreon.com/michaelpennmath Merch: https://teespring.com/stores/michael-penn-math My amazon shop: https://www.amazon.com/shop/michaelpenn 🟢 Discord: https://discord.gg/Ta6PTGtKBm ⭐my other channels⭐ Main Channel: https://www.youtube.
From playlist Abstract Algebra

Lie Groups and Lie Algebras: Lesson 44 Group Theory Review #3 (corrected!)
Lie Groups and Lie Algebras: Lesson 44 Group Theory Review #3 This is a corrected version of a previous upload. In the earlier version I ridiculously stated that cyclic subgroups were normal. I don't know what came over me, that is certainly NOT true. What is true is that if a group is a
From playlist Lie Groups and Lie Algebras

Lagrange's Theorem and Index of Subgroups | Abstract Algebra
We introduce Lagrange's theorem, showing why it is true and follows from previously proven results about cosets. We also investigate groups of prime order, seeing how Lagrange's theorem informs us about every group of prime order - in particular it tells us that any group of prime order p
From playlist Abstract Algebra

Visual Group Theory, Lecture 4.5: The isomorphism theorems
Visual Group Theory, Lecture 4.5: The isomorphism theorems There are four central results in group theory that are collectively known at the isomorphism theorems. We introduced the first of these a few lectures back, under the name of the "fundamental homomorphism theorem." In this lectur
From playlist Visual Group Theory
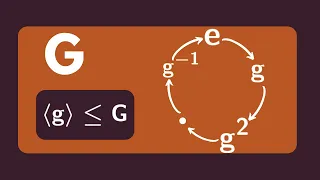
Abstract Algebra | Cyclic Subgroups
We define the notion of a cyclic subgroup and give a few examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Visual Group Theory, Lecture 5.3: Examples of group actions
Visual Group Theory, Lecture 5.3: Examples of group actions It is frequently of interest to analyze the action of a group on its elements (by multiplication), subgroups (by multiplication, or by conjugation), or cosets (by multiplication). We look at all of these, and analyze the orbits,
From playlist Visual Group Theory