
More Standard Deviation and Variance
Further explanations and examples of standard deviation and variance
From playlist Unit 1: Descriptive Statistics

Statistics Lecture 3.3: Finding the Standard Deviation of a Data Set
https://www.patreon.com/ProfessorLeonard Statistics Lecture 3.3: Finding the Standard Deviation of a Data Set
From playlist Statistics (Full Length Videos)

One Variable Statistics Using a Free Online App (MOER/MathAS)
This video explains how to use a free online app similar to the TI84 to determine one variable statistics. https://oervm.s3-us-west-2.amazonaws.com/tvm/indexStats.html
From playlist Statistics: Describing Data

Percentiles, Deciles, Quartiles
Understanding percentiles, quartiles, and deciles through definitions and examples
From playlist Unit 1: Descriptive Statistics
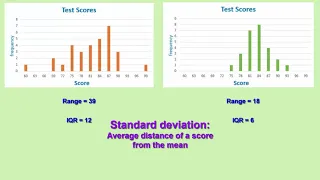
Introduction to standard deviation, IQR [Inter-Quartile Range], and range
From playlist Unit 1: Descriptive Statistics

Micrometer/diameter of daily used objects.
What was the diameter? music: https://www.bensound.com/
From playlist Fine Measurements
Data that are collected for statistical analysis can be classified according to their type. It is important to know what data type we are dealing with as this determines the type of statistical test to use.
From playlist Learning medical statistics with python and Jupyter notebooks

Sloppiness and Parameter Identifiability, Information Geometry by Mark Transtrum
26 December 2016 to 07 January 2017 VENUE: Madhava Lecture Hall, ICTS Bangalore Information theory and computational complexity have emerged as central concepts in the study of biological and physical systems, in both the classical and quantum realm. The low-energy landscape of classical
From playlist US-India Advanced Studies Institute: Classical and Quantum Information

Guido Montúfar : Fisher information metric of the conditional probability politopes
Recording during the thematic meeting : "Geometrical and Topological Structures of Information" the September 01, 2017 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent
From playlist Geometry

Measuring Variation: Range and Standard Deviation
This lesson explains how to determine the range and standard deviation for a set of data. Site: http://mathispower4u.com
From playlist Statistics: Describing Data

Why do simple models work? Partial answers from information geometry (Lecture 1) by Ben Machta
26 December 2016 to 07 January 2017 VENUE: Madhava Lecture Hall, ICTS Bangalore Information theory and computational complexity have emerged as central concepts in the study of biological and physical systems, in both the classical and quantum realm. The low-energy landscape of classical
From playlist US-India Advanced Studies Institute: Classical and Quantum Information

Introduction to Geometer's Sketchpad: Measurements
This video demonstrates some of the measurement and calculation features of Geometer's Sketchpad.
From playlist Geometer's Sketchpad

On support localisation, the Fisher metric and optimal sampling .. - Poon - Workshop 1 - CEB T1 2019
Poon (University of Bath/Cambridge) / 06.02.2019 On support localisation, the Fisher metric and optimal sampling in off-the-grid sparse regularisation Sparse regularization is a central technique for both machine learning and imaging sciences. Existing performance guarantees assume a se
From playlist 2019 - T1 - The Mathematics of Imaging

Alice Le Brigant : Information geometry and shape analysis for radar signal processing
Recording during the thematic meeting : "Geometrical and Topological Structures of Information" the August 31, 2017 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent
From playlist Geometry

Wuchen Li: "Accelerated Information Gradient Flow"
High Dimensional Hamilton-Jacobi PDEs 2020 Workshop II: PDE and Inverse Problem Methods in Machine Learning "Accelerated Information Gradient Flow" Wuchen Li - University of California, Los Angeles (UCLA) Abstract: We present a systematic framework for the Nesterov's accelerated gradient
From playlist High Dimensional Hamilton-Jacobi PDEs 2020

Shannon 100 - 27/10/2016 - Anne AUGER
How information theory sheds new light on black-box optimization Anne Auger (INRIA) Black-box optimization problems occur frequently in many domains ranging from engineering to biology or medicine. In black-box optimization, no information on the function to be optimized besides current
From playlist Shannon 100

Frédéric Barbaresco - Le radar digital...
Frédéric Barbaresco - Le radar digital ou les structures géométriques élémentaires de l’information électromagnétique Conférence donnée devant L'Association des Amis de l'IHES à l'IHES le 9 mars 2017. Frédéric Barbaresco, représentant KTD Board Processing, Computing & Cognition auprès d
From playlist Évenements grand public

(PP 6.4) Density for a multivariate Gaussian - definition and intuition
The density of a (multivariate) non-degenerate Gaussian. Suggestions for how to remember the formula. Mathematical intuition for how to think about the formula.
From playlist Probability Theory

Computational Differential Geometry, Optimization Algorithms by Mark Transtrum
26 December 2016 to 07 January 2017 VENUE: Madhava Lecture Hall, ICTS Bangalore Information theory and computational complexity have emerged as central concepts in the study of biological and physical systems, in both the classical and quantum realm. The low-energy landscape of classical
From playlist US-India Advanced Studies Institute: Classical and Quantum Information
