Gibbs measure

Measures (measure theory) | Game theory equilibrium concepts

In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is a generalization of the canonical ensemble to infinite systems. The canonical ensemble gives the probability of the system X being in state x (equivalently, of the random variable X having value x) as Here, E is a function from the space of states to the real numbers; in physics applications, E(x) is interpreted as the energy of the configuration x. The parameter β is a free parameter; in physics, it is the inverse temperature. The normalizing constant Z(β) is the partition function. However, in infinite systems, the total energy is no longer a finite number and cannot be used in the traditional construction of the probability distribution of a canonical ensemble. Traditional approaches in statistical physics studied the limit of intensive properties as the size of a finite system approaches infinity (the thermodynamic limit). When the energy function can be written as a sum of terms that each involve only variables from a finite subsystem, the notion of a Gibbs measure provides an alternative approach. Gibbs measures were proposed by probability theorists such as Dobrushin, Lanford, and Ruelle and provided a framework to directly study infinite systems, instead of taking the limit of finite systems. A measure is a Gibbs measure if the conditional probabilities it induces on each finite subsystem satisfy a consistency condition: if all degrees of freedom outside the finite subsystem are frozen, the canonical ensemble for the subsystem subject to these boundary conditions matches the probabilities in the Gibbs measure conditional on the frozen degrees of freedom. The Hammersley–Clifford theorem implies that any probability measure that satisfies a Markov property is a Gibbs measure for an appropriate choice of (locally defined) energy function. Therefore, the Gibbs measure applies to widespread problems outside of physics, such as Hopfield networks, Markov networks, Markov logic networks, and boundedly rational potential games in game theory and economics. A Gibbs measure in a system with local (finite-range) interactions maximizes the entropy density for a given expected energy density; or, equivalently, it minimizes the free energy density. The Gibbs measure of an infinite system is not necessarily unique, in contrast to the canonical ensemble of a finite system, which is unique. The existence of more than one Gibbs measure is associated with statistical phenomena such as symmetry breaking and phase coexistence. (Wikipedia).

Statistics Lecture 3.3: Finding the Standard Deviation of a Data Set

https://www.patreon.com/ProfessorLeonard Statistics Lecture 3.3: Finding the Standard Deviation of a Data Set

From playlist Statistics (Full Length Videos)

Inverse normal with Z Table

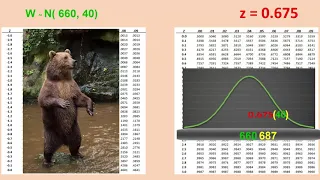
Determining values of a variable at a particular percentile in a normal distribution

From playlist Unit 2: Normal Distributions

More Standard Deviation and Variance

Further explanations and examples of standard deviation and variance

From playlist Unit 1: Descriptive Statistics

How to find the number of standard deviations that it takes to represent all the data

👉 Learn how to find the variance and standard deviation of a set of data. The variance of a set of data is a measure of spread/variation which measures how far a set of numbers is spread out from their average value. The standard deviation of a set of data is a measure of spread/variation

From playlist Variance and Standard Deviation

Intro to Sample Proportions

An overview and introduction to understanding sampling distributions of proportions [sample proportions] and how to calculate them

From playlist Unit 7 Probability C: Sampling Distributions & Simulation

Percentiles, Deciles, Quartiles

Understanding percentiles, quartiles, and deciles through definitions and examples

From playlist Unit 1: Descriptive Statistics

Learning how to find the variance and standard deviation from a set of data

From playlist Variance and Standard Deviation

How to find the variance and standard deviation from a set of data

From playlist Variance and Standard Deviation

Measures of Center

This video is about the measures of center, including the mean, median, and mode.

From playlist Statistical Measures

The Sherrington-Kirkpatrick model and its diluted version II

Dmitry Panchenko Texas A&M University March 12, 2014 I will talk about two types of random processes -- the classical Sherrington-Kirkpatrick (SK) model of spin glasses and its diluted version. One of the main goals in these models is to find a formula for the maximum of the process, or th

From playlist Mathematics

Codina Cotar: Disorder relevance for non-convex random gradient Gibbs measures in d ≤ 2

HYBRID EVENT Recorded during the meeting " Probability/PDE Interactions: Interface Models and Particle Systems " the April 28, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by world

From playlist Probability and Statistics

Gérard Ben Arous: Geometric description of the spherical Spin-Glass Gibbs measures and...

Abstract: The Gibbs measure of many disordered systems at low temperature may exhibit a very strong dependance on even tiny variations of temperature, usually called “temperature chaos”. I will discuss this question for Spin Glasses. I will report on a recent work with Eliran Subag (Couran

From playlist Probability and Statistics

The Sherrington-Kirkpatrick model and its diluted version I - Dmitry Panchenko - Dmitry Panchenko

From playlist Mathematics

Eric Endo

From playlist Contributed talks One World Symposium 2020

Quasicrystal Phases in a Finite-Range Lattice Gas Model - Siamak Taati

From playlist Mathematics of Condensed Matter and Beyond (February 22-25, 2021)

Vaughn Climenhaga: Beyond Bowen specification property - lecture 1

Rufus Bowen introduced the specification property for uniformly hyperbolic dynamical systems and used it to establish uniqueness of equilibrium states, including the measure of maximal entropy. After reviewing Bowen's argument, we will present our recent work on extending Bowen's approach

From playlist Dynamical Systems and Ordinary Differential Equations

Luisa Borsato

From playlist Contributed talks One World Symposium 2020

Discussion Meeting

PROGRAM: Nonlinear filtering and data assimilation DATES: Wednesday 08 Jan, 2014 - Saturday 11 Jan, 2014 VENUE: ICTS-TIFR, IISc Campus, Bangalore LINK:http://www.icts.res.in/discussion_meeting/NFDA2014/ The applications of the framework of filtering theory to the problem of data assimi

From playlist Nonlinear filtering and data assimilation

Measures of Spread Overview

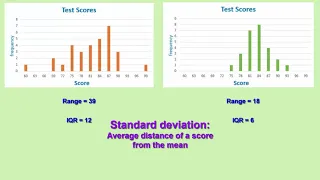
Introduction to standard deviation, IQR [Inter-Quartile Range], and range

From playlist Unit 1: Descriptive Statistics

Wei Wu -- Massless phases for the Villain model in dimension 3 and greater

The XY and the Villain models are mathematical idealization of real world models of liquid crystal, liquid helium, and superconductors. Their phase transition has important applications in condensed matter physics and led to the Nobel Prize in Physics in 2016. However we are still far from

From playlist Columbia Probability Seminar

Gibbs measure

Related pages