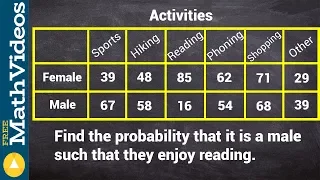
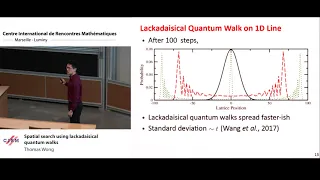
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number used for describing the behaviour of systems. The modulus squared of this quantity represents a probability density. Probability amplitudes provide a relationship between the quantum state vector of a system and the results of observations of that system, a link was first proposed by Max Born, in 1926. Interpretation of values of a wave function as the probability amplitude is a pillar of the Copenhagen interpretation of quantum mechanics. In fact, the properties of the space of wave functions were being used to make physical predictions (such as emissions from atoms being at certain discrete energies) before any physical interpretation of a particular function was offered. Born was awarded half of the 1954 Nobel Prize in Physics for this understanding, and the probability thus calculated is sometimes called the "Born probability". These probabilistic concepts, namely the probability density and quantum measurements, were vigorously contested at the time by the original physicists working on the theory, such as Schrödinger and Einstein. It is the source of the mysterious consequences and philosophical difficulties in the interpretations of quantum mechanics—topics that continue to be debated even today. (Wikipedia).