
What is a Manifold? Lesson 6: Topological Manifolds
Topological manifolds! Finally! I had two false starts with this lesson, but now it is fine, I think.
From playlist What is a Manifold?

What is a Manifold? Lesson 2: Elementary Definitions
This lesson covers the basic definitions used in topology to describe subsets of topological spaces.
From playlist What is a Manifold?

Manifolds 1.3 : More Examples (Animation Included)
In this video, I introduce the manifolds of product manifolds, tori/the torus, real vectorspaces, matrices, and linear map spaces. This video uses a math animation for visualization. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : http://docdro.id/5koj5
From playlist Manifolds

I define topological manifolds. Motivated by the prospect of calculus on topological manifolds, I introduce smooth manifolds. At the end I point out how one needs to change the definitions, to obtain C^1 or even complex manifolds. To learn more about manifolds, see Lee's "Introduction to
From playlist Differential geometry

Manifolds 1.2 : Examples of Manifolds
In this video, I describe basic examples of manifolds. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : http://docdro.id/IZO0G25
From playlist Manifolds
What is a Manifold? Lesson 8: Diffeomorphisms
What is a Manifold? Lesson 8: Diffeomorphisms
From playlist What is a Manifold?

Manifolds 1.1 : Basic Definitions
In this video, I give the basic intuition and definitions of manifolds. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Manifolds

Today, we take a look at atlases, provide an example for the circle, and discuss different types of atlases we may wish to have on our manifold.
From playlist Manifolds

Hao Xu (7/26/22): Frobenius algebra structure of statistical manifold
Abstract: In information geometry, a statistical manifold is a Riemannian manifold (M,g) equipped with a totally symmetric (0,3)-tensor. We show that the tangent bundle of a statistical manifold has a Frobenius algebra structure if and only if the sectional K-curvature vanishes. This gives
From playlist Applied Geometry for Data Sciences 2022

Noémie Combe - How many Frobenius manifolds are there?
In this talk an overview of my recent results is presented. In a joint work with Yu. Manin (2020) we discovered that an object central to information geometry: statistical manifolds (related to exponential families) have an F-manifold structure. This algebraic structure is a more general v
From playlist Research Spotlight

Haim Sompolinsky: "Statistical Mechanics of Deep Manifolds: Mean Field Geometry in High Dimension"
Machine Learning for Physics and the Physics of Learning 2019 Workshop IV: Using Physical Insights for Machine Learning "Statistical Mechanics of Deep Manifolds: Mean Field Geometry in High Dimension" Haim Sompolinsky - The Hebrew University of Jerusalem Abstract: Recent advances in sys
From playlist Machine Learning for Physics and the Physics of Learning 2019

DDPS | Data-driven information geometry approach to stochastic model reduction
Description: Reduced-order models are often obtained by projection onto a subspace; standard least squares in linear spaces is a familiar technique that can also be applied to stochastic phenomena as exemplified by polynomial chaos expansions. Optimal approximants are obtained by minimizin
From playlist Data-driven Physical Simulations (DDPS) Seminar Series

Alain Trouvé et Xavier Pennec : Minicourse Shape Spaces and Geometric Statistics
Recording during the thematic meeting : "Geometrical and Topological Structures of Information" the August 31, 2017 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematician
From playlist Geometry

Capturing Turbulent Dynamics and Statistics in Experiments using Exact.... by Balachandra Suri
SEMINAR Capturing Turbulent Dynamics and Statistics in Experiments using Exact Coherent States Speaker: Balachandra Suri (Institute of Science and Technology, Austria) Date: Thursday, 21 January 2021, Venue: Online seminar Turbulence is widely regarded as the last unsolved pro
From playlist Seminar Series

Alice Le Brigant : Information geometry and shape analysis for radar signal processing
Recording during the thematic meeting : "Geometrical and Topological Structures of Information" the August 31, 2017 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent
From playlist Geometry

Marc Mézard: "Machine learning with neural networks: the importance of data structure"
Machine Learning for Physics and the Physics of Learning 2019 Workshop IV: Using Physical Insights for Machine Learning "Machine learning with neural networks: the importance of data structure" Marc Mézard - Ecole Normale Supérieure Abstract: The success of deep neural networks still
From playlist Machine Learning for Physics and the Physics of Learning 2019

The discrete Gaussian free field on a compact manifold by Alessandra Cipriani
PROGRAM :UNIVERSALITY IN RANDOM STRUCTURES: INTERFACES, MATRICES, SANDPILES ORGANIZERS :Arvind Ayyer, Riddhipratim Basu and Manjunath Krishnapur DATE & TIME :14 January 2019 to 08 February 2019 VENUE :Madhava Lecture Hall, ICTS, Bangalore The primary focus of this program will be on the
From playlist Universality in random structures: Interfaces, Matrices, Sandpiles - 2019

A hitchin-kobayashi correspondance for generalized seiberg-witten equations by Varun Thakre
Program : Integrable systems in Mathematics, Condensed Matter and Statistical Physics ORGANIZERS : Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE & TIME : 16 July 2018 to 10 August 2018 VENUE : Ramanujan L
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

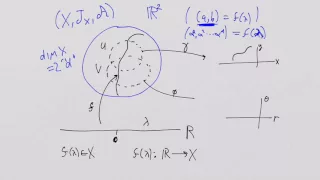
Manifolds #4: Differentiability
Today, we take a look at a look at how to define the differentiability of a function involving a manifold. This will allow us to define the notion of a tangent vector space in the following video.
From playlist Manifolds
