Field Theory: Definition/ Axioms
This video is about the basics axioms of fields.
From playlist Basics: Field Theory
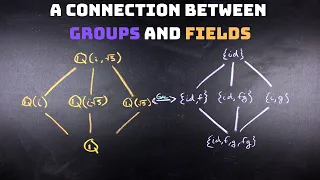
The Structure of Fields: What is a field and a connection between groups and fields
This video is primarily meant to help develop some ideas around the structure of fields and a connection between groups and fields (which will allow me to create more abstract algebra videos in the future! 😀😅🤓) 00:00 Intro 01:04 What is a Field? Here we give the definition of a field in
From playlist The New CHALKboard

Definition of a Field In this video, I define the concept of a field, which is basically any set where you can add, subtract, add, and divide things. Then I show some neat properties that have to be true in fields. Enjoy! What is an Ordered Field: https://youtu.be/6mc5E6x7FMQ Check out
From playlist Real Numbers

This video is about polynomials with coefficients in a field.
From playlist Basics: Field Theory

Fields - Field Theory - Lecture 00
This is the first in a series of videos for my abstract algebra class during the 2020 shutdown. This lecture is intended to rapidly catch students up who are going to follow online and aren't from UVM. We are using Dummit and Foote.
From playlist Field Theory
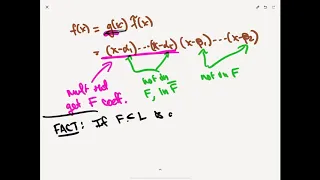
Field Theory - (optional) Primitive Element Theorem - Lecture 15
For finite extensions L \supset F we show that there exists an element \gamma in L such that F(\gamma) = L. This is called the primitive element theorem.
From playlist Field Theory

Field Theory - Algebraically Closed Fields - Lecture 9
In this video we define what an algebraically closed field and assert without proof that they exist. We also explain why if you can find a single root for any polynomial, then you can find them all.
From playlist Field Theory
Field Theory: Fields of Order a Power of a Prime
This video is about finite fields and some of their properties.
From playlist Basics: Field Theory

A Short Course in Algebra and Number Theory - Fields
To supplement a course taught at The University of Queensland's School of Mathematics and Physics I present a very brief summary of algebra and number theory for those students who need to quickly refresh that material or fill in some gaps in their understanding. This is the third lectur
From playlist A Short Course in Algebra and Number Theory

This lecture is part of an online graduate course on Galois theory. We use the theory of splitting fields to classify finite fields: there is one of each prime power order (up to isomorphism). We give a few examples of small order, and point out that there seems to be no good choice for
From playlist Galois theory

Lecture 34. Galois groups and fixed fields
From playlist Abstract Algebra 2

Lecture 30. Fields, field extensions
0:00 Fields 1:48 Examples of fields 08:20 Characteristic of a field 11:20 Prime subfields (Q, F_p) 12:00 Every field has a prime subfield; relation of prime subfield to characteristic 20:15 Frobenius homomorphism 22:40 Field extension 23:50 A field extension of K possesses a structure of
From playlist Abstract Algebra 2

Introduction to number theory lecture 30. Fields in number theory
This lecture is part of my Berkeley math 115 course "Introduction to number theory" For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj53L8sMbzIhhXSAOpuZ1Fov8 We extend some of the results we proved about the integers mod p to more general fields.
From playlist Introduction to number theory (Berkeley Math 115)
Cryptography and Network Security by Prof. D. Mukhopadhyay, Department of Computer Science and Engineering, IIT Kharagpur. For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist Computer - Cryptography and Network Security

RNT2.1.1. Finite Fields of Orders 4 and 8
Ring Theory: As an application of maximal ideals and residue fields, we give explicit constructions of fields with 4 and 8 elements. A key step is to find irreducible polynomials (quadratic and cubic).
From playlist Abstract Algebra

Lec 8 | MIT 6.451 Principles of Digital Communication II
Introduction to Finite Fields View the complete course: http://ocw.mit.edu/6-451S05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.451 Principles of Digital Communication II

Shaoshi Chen, Chinese Academy of Sciences
May 3, Shaoshi Chen, Chinese Academy of Sciences Stability Problems in Symbolic Integration
From playlist Spring 2022 Online Kolchin seminar in Differential Algebra

Algebra 1M - international Course no. 104016 Dr. Aviv Censor Technion - International school of engineering
From playlist Algebra 1M