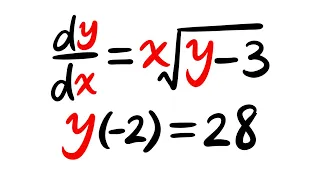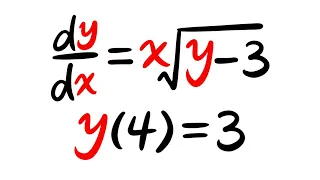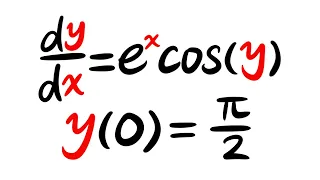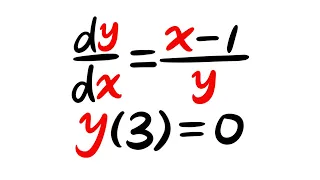Approximation algorithms | Computational hardness assumptions | Unsolved problems in computer science | Computational complexity theory | Conjectures
Unique games conjecture
In computational complexity theory, the unique games conjecture (often referred to as UGC) is a conjecture made by Subhash Khot in 2002. The conjecture postulates that the problem of determining the approximate value of a certain type of game, known as a unique game, has NP-hard computational complexity. It has broad applications in the theory of hardness of approximation. If the unique games conjecture is true and P ≠ NP, then for many important problems it is not only impossible to get an exact solution in polynomial time (as postulated by the P versus NP problem), but also impossible to get a good polynomial-time approximation. The problems for which such an inapproximability result would hold include constraint satisfaction problems, which crop up in a wide variety of disciplines. The conjecture is unusual in that the academic world seems about evenly divided on whether it is true or not. (Wikipedia).