Filtration (mathematics)

Measure theory | Algebra | Stochastic processes

In mathematics, a filtration is an indexed family of subobjects of a given algebraic structure , with the index running over some totally ordered index set , subject to the condition that if in , then . If the index is the time parameter of some stochastic process, then the filtration can be interpreted as representing all historical but not future information available about the stochastic process, with the algebraic structure gaining in complexity with time. Hence, a process that is adapted to a filtration is also called non-anticipating, because it cannot "see into the future". Sometimes, as in a filtered algebra, there is instead the requirement that the be subalgebras with respect to some operations (say, vector addition), but not with respect to other operations (say, multiplication) that satisfy only , where the index set is the natural numbers; this is by analogy with a graded algebra. Sometimes, filtrations are supposed to satisfy the additional requirement that the union of the be the whole , or (in more general cases, when the notion of union does not make sense) that the canonical homomorphism from the direct limit of the to is an isomorphism. Whether this requirement is assumed or not usually depends on the author of the text and is often explicitly stated. This article does not impose this requirement. There is also the notion of a descending filtration, which is required to satisfy in lieu of (and, occasionally, instead of ). Again, it depends on the context how exactly the word "filtration" is to be understood. Descending filtrations are not to be confused with the dual notion of cofiltrations (which consist of quotient objects rather than subobjects). Filtrations are widely used in abstract algebra, homological algebra (where they are related in an important way to spectral sequences), and in measure theory and probability theory for nested sequences of σ-algebras. In functional analysis and numerical analysis, other terminology is usually used, such as or . (Wikipedia).

Evaluate an expression with three variables

👉 Learn how to evaluate mathematics expressions. A mathematics expression is a finite combination of numbers and symbols formed following a set of operations or rules. To evaluate a mathematics expression means to obtain the solution to the expression given the value(s) of the variable(s)

From playlist Simplify Expressions Using Order of Operations

Evaluate an expression with one variable ex2, 2x + 3 - 2; x=5

From playlist Simplify Expressions Using Order of Operations

Applying distributive property with a negative one to solve the multi step equation

👉 Learn how to solve multi-step equations with parenthesis. An equation is a statement stating that two values are equal. A multi-step equation is an equation which can be solved by applying multiple steps of operations to get to the solution. To solve a multi-step equation with parenthes

From playlist How to Solve Multi Step Equations with Parenthesis

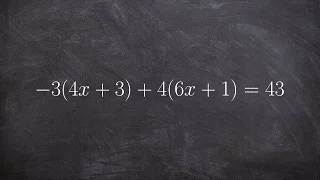
Using Distributive property twice and combining like terms to solve for x

From playlist How to Solve Multi Step Equations with Parenthesis

Evaluating mathematical expressions

From playlist Simplify Expressions Using Order of Operations

The Difference Between an Expression and an Equation

This video explains the difference between an expression and an equation. Site: http://mathispower4u.com Blog: http://mathispower4u.wordpress.com

From playlist Introduction to Linear Equations in One Variable

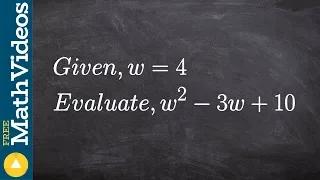
Evaluating an expression with one variable ex 7, w^2 - 3w + 10; w = 4

From playlist Simplify Expressions Using Order of Operations

NEW TOPOLOGICAL LAYER in Graph Neural Networks (GCN), Filtrations, Persistent Homology - ICLR 2022

NEW: integrate a topological layer as one of the Graph Convolutional Network (GCN) layer in to your GCN to obtain essential topological info about the Graph. Persistent Homology, Learnable Filtrations and Topology. Topological Data Analysis (TDA). Although this method is limited to l=1, c

From playlist Learn Graph Neural Networks: code, examples and theory

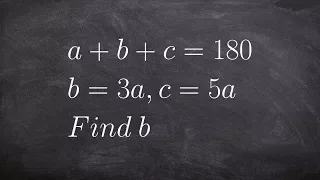
Evaluate an equation by substitution

From playlist Simplify Expressions Using Order of Operations

Models from Biomathematics (Lecture 2) by Hari Shankar Mahato

PROGRAM: MULTI-SCALE ANALYSIS AND THEORY OF HOMOGENIZATION ORGANIZERS: Patrizia Donato, Editha Jose, Akambadath Nandakumaran and Daniel Onofrei DATE: 26 August 2019 to 06 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Homogenization is a mathematical procedure to understa

From playlist Multi-scale Analysis And Theory Of Homogenization 2019

Solving an equation with variables on both side and one solution

👉 Learn how to solve multi-step equations with variable on both sides of the equation. An equation is a statement stating that two values are equal. A multi-step equation is an equation which can be solved by applying multiple steps of operations to get to the solution. To solve a multi-s

From playlist Solve Multi-Step Equations......Help!

Thirteenth SIAM Activity Group on FME Virtual Talk

Speakers: Damir Filipovic, EPFL and Swiss Finance Institute Title: A Machine Learning Approach to Portfolio Pricing and Risk Management for High-Dimensional Problems Moderator: Rene Carmona, Princeton University

From playlist SIAM Activity Group on FME Virtual Talk Series

Christophe Leuridan: Filtrations polyadiques, complémentabilité, maximalité

Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b

From playlist Probability and Statistics

Interactive visualization of 2-D persistence modules - Lesnick

Michael Lesnick Columbia University November 7, 2015 In topological data analysis, we often study data by associating to the data a filtered topological space, whose structure we can then examine using persistent homology. However, in many settings, a single filtered space is not a rich en

From playlist Mathematics

Heather Harrington (12/10/18): Multi-parameter persistent homology and applications

Multi-parameter persistent homology and applications

From playlist AATRN 2018

Beyond geometric invariant theory 2: Good moduli spaces, and applications by Daniel Halpern-Leistner

DISCUSSION MEETING: MODULI OF BUNDLES AND RELATED STRUCTURES ORGANIZERS : Rukmini Dey and Pranav Pandit DATE: 10 February 2020 to 14 February 2020 VENUE: Ramanujan Lecture Hall, ICTS, Bangalore Background: At its core, much of mathematics is concerned with the problem of classifying

From playlist Moduli Of Bundles And Related Structures 2020

Jeremy Hahn : Prismatic and syntomic cohomology of ring spectra

CONFERENCE Recording during the thematic meeting : « Chromatic Homotopy, K-Theory and Functors» the January 24, 2023 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Jean Petit Find this video and other talks given by worldwide mathematicians on CIR

From playlist Topology

On the notion of Î»-connection - Carlos Simpson

Geometry and Arithmetic: 61st Birthday of Pierre Deligne Carlos Simpson University of Nice October 18, 2005 Pierre Deligne, Professor Emeritus, School of Mathematics. On the occasion of the sixty-first birthday of Pierre Deligne, the School of Mathematics will be hosting a four-day confe

From playlist Pierre Deligne 61st Birthday

Evaluating an expression with one variable ex 4, x - 3 - 7x; x = 10

From playlist Simplify Expressions Using Order of Operations

Andrew Lobb: Quantum sln knot cohomology and the slice genus

Abstract: We will give an overview of the information about the smooth slice genus so far yielded by the quantum 𝔰𝔩n knot cohomologies. Recording during the thematic meeting "Knotted Embeddings in Dimensions 3 and 4" the February 15, 2017 at the Centre International de Rencontres Mathémat

From playlist Topology

Filtration (mathematics)

Related pages