
Introduction to the Dirac Delta Function
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Introduction to the Dirac Delta Function
From playlist Differential Equations

From the Dirac Lagrangian to the Dirac Equations | Non-Interacting Lagrangian Density
In this video, we continue with the Dirac Lagrangian which describes spin-1/2 particles in #QuantumMechanics and show how to get the Dirac equation using the Euler-Lagrange equations! If you want to read more about the Dirac equation, we can recommend the book „An Introduction to Quantum
From playlist Dirac Equation

Gamma Matrices in Action #2 | How to do Calculations with Gamma Matrices
In this video, we show you how to use Dirac’s gamma matrices to do calculations in relativistic #QuantumMechanics! If you want to read more about the gamma matrices, we can recommend the book „An Introduction to Quantum Field Theory“ by Michael Peskin and Daniel Schroeder, especially cha
From playlist Dirac Equation

Dirac Equation | Gamma Matrices
▶ Topics ◀ Gamma Matrices, Dirac Equation, Clifford Algebra, Anti Commutator ▶ Social Media ◀ [Instagram] @prettymuchvideo ▶ Music ◀ TheFatRat - Fly Away feat. Anjulie https://open.spotify.com/track/1DfFHyrenAJbqsLcpRiOD9 If you want to help us get rid of ads on YouTube, you can suppor
From playlist Dirac Equation

Dirac delta function | Lecture 33 | Differential Equations for Engineers
Definition of the Dirac delta function and its Laplace transform. Join me on Coursera: https://www.coursera.org/learn/differential-equations-engineers Lecture notes at http://www.math.ust.hk/~machas/differential-equations-for-engineers.pdf Subscribe to my channel: http://www.youtube.co
From playlist Differential Equations for Engineers

Quantum Mechanics 12a - Dirac Equation I
When quantum mechanics and relativity are combined to describe the electron the result is the Dirac equation, presented in 1928. This equation predicts electron spin and the existence of anti-matter.
From playlist Quantum Mechanics
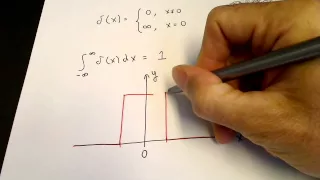
Explanation of the Dirac delta function and its Laplace transform. Join me on Coursera: Matrix Algebra for Engineers: https://www.coursera.org/learn/matrix-algebra-engineers Differential Equations for Engineers: https://www.coursera.org/learn/differential-equations-engineers Vector Ca
From playlist Differential Equations

(ML 7.7.A1) Dirichlet distribution
Definition of the Dirichlet distribution, what it looks like, intuition for what the parameters control, and some statistics: mean, mode, and variance.
From playlist Machine Learning

Gamma Matrices and the Clifford Algebra
In this video, we show you how to use Dirac’s gamma matrices to do calculations in relativistic #QuantumMechanics! If you want to read more about the gamma matrices, we can recommend the book „An Introduction to Quantum Field Theory“ by Michael Peskin and Daniel Schroeder, especially cha
From playlist Dirac Equation

QED Prerequisites: The Dirac Equation
In this lesson we give an introduction to the discovery and logic of the Dirac Equation. We introduce the notion of a 4-component spinor field and Dirac Matrices. We do not start developing a solution for this equation, or for the Klein Gordon equation either. There is much more to say abo
From playlist QED- Prerequisite Topics

Paul Dirac and the religion of mathematical beauty
Speaker: Graham Farmelo Filmed at The Royal Society, London on Fri 04 Mar 2011 1pm - 2pm http://royalsociety.org/events/2011/paul-dirac/
From playlist Popular talks and lectures

Quantum Mechanics 12b - Dirac Equation II
Here we explore solutions to the Dirac equation corresponding to electrons at rest, in uniform motion and within a hydrogen atom. Part 1: https://youtu.be/OCuaBmAzqek
From playlist Quantum Mechanics

Richard Kerner - Unifying Colour SU(3) with Z3-Graded Lorentz-Poincaré Algebra
A generalization of Dirac’s equation is presented, incorporating the three-valued colour variable in a way which makes it intertwine with the Lorentz transformations. We show how the Lorentz-Poincaré group must be extended to accomodate both SU(3) and the Lorentz transformations. Both symm
From playlist Combinatorics and Arithmetic for Physics: 02-03 December 2020

Ginestra Bianconi (8/28/21): The topological Dirac operator and the dynamics of topological signals
Topological signals associated not only to nodes but also to links and to the higher dimensional simplices of simplicial complexes are attracting increasing interest in signal processing, machine learning and network science. Typically, topological signals of a given dimension are investig
From playlist Beyond TDA - Persistent functions and its applications in data sciences, 2021

Quantum Mechanics 12c - Dirac Equation III
Negative-energy solutions seem to invalidate the Dirac equation. Dirac's bold solution led to the prediction of anti-matter. part b: https://youtu.be/tR6UebCvFqE Quantum field theory playlist: https://youtube.com/playlist?list=PLsp_BbZBIk_6_5pi9tHHmoVJzjqpfBkgJ
From playlist Quantum Mechanics

Solving the Dirac Equation | Rest Frame
In this video, we will show you how to solve the Dirac equation. For now, we will focus on the rest frame of the particle. We will show you in a different video how to arrive at general solutions. 00:00 Review of Dirac Equation 00:33 Plane Wave Ansatz 02:06 Rest Frame 02:41 Dirac Rep. 0
From playlist Quantum Mechanics, Quantum Field Theory

Lecture 6 | New Revolutions in Particle Physics: Basic Concepts
(November 9, 2009) Leonard Susskind gives the sixth lecture of a three-quarter sequence of courses that will explore the new revolutions in particle physics. In this lecture he continues on the subject of quantum field theory, including, the diary equation and Higgs Particles. Leonard S
From playlist Lecture Collection | Particle Physics: Basic Concepts
