
Number Theory 1.2 : The Gamma Function
In this video, I introduce the gamma function and show a few properties of it. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Number Theory

Gamma Matrices in Action #2 | How to do Calculations with Gamma Matrices
In this video, we show you how to use Dirac’s gamma matrices to do calculations in relativistic #QuantumMechanics! If you want to read more about the gamma matrices, we can recommend the book „An Introduction to Quantum Field Theory“ by Michael Peskin and Daniel Schroeder, especially cha
From playlist Dirac Equation

The Gamma Function for Half Integer Values
Help me create more free content! =) https://www.patreon.com/mathable Merch :v - https://teespring.com/de/stores/papaflammy https://www.amazon.com/shop/flammablemaths https://shop.spreadshirt.de/papaflammy Reflection Formula: https://www.youtube.com/wa
From playlist Number Theory
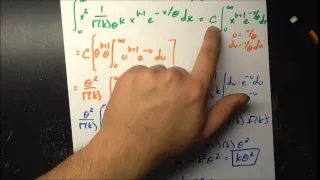
From playlist Probability Distributions

Gamma Matrices in Action #1 | How to do Calculations with Gamma Matrices
In this video, we show you how to use Dirac’s gamma matrices to do calculations in relativistic #QuantumMechanics! If you want to read more about the gamma matrices, we can recommend the book „An Introduction to Quantum Field Theory“ by Michael Peskin and Daniel Schroeder, especially cha
From playlist Dirac Equation

Gamma Matrices and the Clifford Algebra
In this video, we show you how to use Dirac’s gamma matrices to do calculations in relativistic #QuantumMechanics! If you want to read more about the gamma matrices, we can recommend the book „An Introduction to Quantum Field Theory“ by Michael Peskin and Daniel Schroeder, especially cha
From playlist Dirac Equation

Linear Algebra for Computer Scientists. 12. Introducing the Matrix
This computer science video is one of a series of lessons about linear algebra for computer scientists. This video introduces the concept of a matrix. A matrix is a rectangular or square, two dimensional array of numbers, symbols, or expressions. A matrix is also classed a second order
From playlist Linear Algebra for Computer Scientists
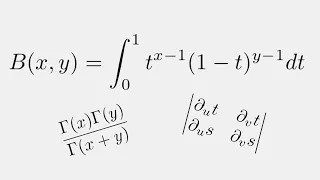
Beta Function - Integral Representation Derivation
Today, we derive the integral representation for the Beta function. We will be using this result in a future video to prove the Euler reflection formula!
From playlist Integrals
Relativity's key concept: Lorentz gamma
Einstein’s theory of special relativity is one of the most counterintuitive ideas in physics, for instance, moving clocks record time differently than stationary ones. Central to all of the equations of relativity is the Lorentz factor, also known as gamma. In this video, Fermilab’s Dr. D
From playlist Relativity

QED Prerequisites: The Dirac Equation
In this lesson we give an introduction to the discovery and logic of the Dirac Equation. We introduce the notion of a 4-component spinor field and Dirac Matrices. We do not start developing a solution for this equation, or for the Klein Gordon equation either. There is much more to say abo
From playlist QED- Prerequisite Topics

Richard Kerner - Unifying Colour SU(3) with Z3-Graded Lorentz-Poincaré Algebra
A generalization of Dirac’s equation is presented, incorporating the three-valued colour variable in a way which makes it intertwine with the Lorentz transformations. We show how the Lorentz-Poincaré group must be extended to accomodate both SU(3) and the Lorentz transformations. Both symm
From playlist Combinatorics and Arithmetic for Physics: 02-03 December 2020
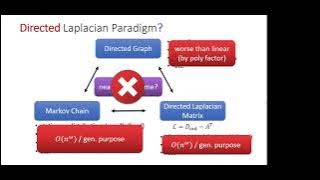
Solving Laplacian Systems of Directed Graphs - John Peebles
Computer Science/Discrete Mathematics Seminar II Topic: Solving Laplacian Systems of Directed Graphs Speaker: John Peebles Affiliation: Member, School of Mathematics Date: March 02, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

Right-angled Coxeter groups and affine actions ( Lecture 01) by Francois Gueritaud
DISCUSSION MEETING SURFACE GROUP REPRESENTATIONS AND PROJECTIVE STRUCTURES ORGANIZERS: Krishnendu Gongopadhyay, Subhojoy Gupta, Francois Labourie, Mahan Mj and Pranab Sardar DATE: 10 December 2018 to 21 December 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore The study of spaces o
From playlist Surface group representations and Projective Structures (2018)

MIT 8.701 Introduction to Nuclear and Particle Physics, Fall 2020 Instructor: Markus Klute View the complete course: https://ocw.mit.edu/8-701F20 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP60Do91PdN978llIsvjKW0au Discussion on how to treat spin in the calculation
From playlist MIT 8.701 Introduction to Nuclear and Particle Physics, Fall 2020

In this tutorial we take a look at elementary matrices. They start life off as identity matrices to which a single elementary row operation is performed. They form the building blocks of Gauss-Jordan elimination. In a future video we will use the to do LU decomposition of matrices.
From playlist Introducing linear algebra

Anosov representations: the basics and maybe more (Lecture 02) by Olivier Guichard
DISCUSSION MEETING SURFACE GROUP REPRESENTATIONS AND PROJECTIVE STRUCTURES ORGANIZERS: Krishnendu Gongopadhyay, Subhojoy Gupta, Francois Labourie, Mahan Mj and Pranab Sardar DATE: 10 December 2018 to 21 December 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore The study of spaces o
From playlist Surface group representations and Projective Structures (2018)
