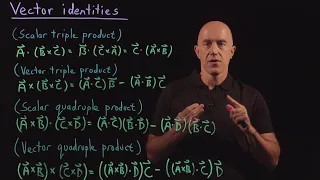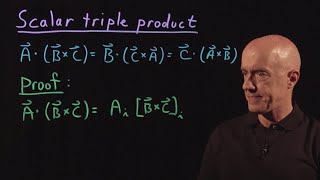Articles containing proofs | Tensors | Linear algebra | Permutations
Levi-Civita symbol
In mathematics, particularly in linear algebra, tensor analysis, and differential geometry, the Levi-Civita symbol or Levi-Civita epsilon represents a collection of numbers; defined from the sign of a permutation of the natural numbers 1, 2, ..., n, for some positive integer n. It is named after the Italian mathematician and physicist Tullio Levi-Civita. Other names include the permutation symbol, antisymmetric symbol, or alternating symbol, which refer to its antisymmetric property and definition in terms of permutations. The standard letters to denote the Levi-Civita symbol are the Greek lower case epsilon ε or ϵ, or less commonly the Latin lower case e. Index notation allows one to display permutations in a way compatible with tensor analysis: where each index i1, i2, ..., in takes values 1, 2, ..., n. There are nn indexed values of εi1i2...in, which can be arranged into an n-dimensional array. The key defining property of the symbol is total antisymmetry in the indices. When any two indices are interchanged, equal or not, the symbol is negated: If any two indices are equal, the symbol is zero. When all indices are unequal, we have: where p (called the parity of the permutation) is the number of pairwise interchanges of indices necessary to unscramble i1, i2, ..., in into the order 1, 2, ..., n, and the factor (−1)p is called the sign or signature of the permutation. The value ε1 2 ... n must be defined, else the particular values of the symbol for all permutations are indeterminate. Most authors choose ε1 2 ... n = +1, which means the Levi-Civita symbol equals the sign of a permutation when the indices are all unequal. This choice is used throughout this article. The term "n-dimensional Levi-Civita symbol" refers to the fact that the number of indices on the symbol n matches the dimensionality of the vector space in question, which may be Euclidean or non-Euclidean, for example, or Minkowski space. The values of the Levi-Civita symbol are independent of any metric tensor and coordinate system. Also, the specific term "symbol" emphasizes that it is not a tensor because of how it transforms between coordinate systems; however it can be interpreted as a tensor density. The Levi-Civita symbol allows the determinant of a square matrix, and the cross product of two vectors in three-dimensional Euclidean space, to be expressed in Einstein index notation. (Wikipedia).