Planar graphs | Circle packing | Theorems about circles | Theorems in graph theory
Circle packing theorem
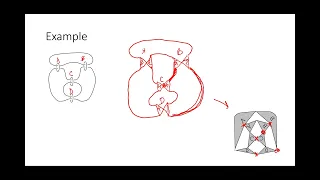
The circle packing theorem (also known as the Koebe–Andreev–Thurston theorem) describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles (in general, on any Riemann surface) whose interiors are disjoint. The intersection graph of a circle packing is the graph having a vertex for each circle, and an edge for every pair of circles that are tangent. If the circle packing is on the plane, or, equivalently, on the sphere, then its intersection graph is called a coin graph; more generally, intersection graphs of interior-disjoint geometric objects are called tangency graphs or contact graphs. Coin graphs are always connected, simple, and planar. The circle packing theorem states that these are the only requirements for a graph to be a coin graph: Circle packing theorem: For every connected simple planar graph G there is a circle packing in the plane whose intersection graph is (isomorphic to) G. (Wikipedia).