
(ML 7.7.A1) Dirichlet distribution
Definition of the Dirichlet distribution, what it looks like, intuition for what the parameters control, and some statistics: mean, mode, and variance.
From playlist Machine Learning

Math 139 Fourier Analysis Lecture 08: Dirichlet Problem on the Unit Disc
Dirichlet problem on the Unit Disc: the problem; the Poisson integral solves the heat equation. L^2 convergence of Fourier Series: definition of L^2 norm; quick review of relevant ideas from linear algebra (vector space, inner product, norm, orthogonal, Pythagorean Theorem, Cauchy-Schwarz
From playlist Course 8: Fourier Analysis

Dirichlet Eta Function - Integral Representation
Today, we use an integral to derive one of the integral representations for the Dirichlet eta function. This representation is very similar to the Riemann zeta function, which explains why their respective infinite series definition is quite similar (with the eta function being an alte rna
From playlist Integrals

Math 139 Fourier Analysis Lecture 35: Dirichlet's theorem pt. 2
Dirichlet's theorem: reduction of the problem. Dirichlet L-function. Product formula for L-functions. Extension of the logarithm to complex numbers. Convergence of infinite products.
From playlist Course 8: Fourier Analysis

Properties of Dirichlet Convolution with Prof. Omar!
Part 2 with Prof. Omar: https://youtu.be/8v_sh7JMUS0 Prof. Omar's video covers a very interesting function called the Möbius function, which has special properties related to the Dirichlet convolution. A video on the fall 2014 Caltech-Harvey Mudd Math Competition (CHMMC) power round prob
From playlist Challenge Problems

(ML 7.7.A2) Expectation of a Dirichlet random variable
How to compute the expected value of a Dirichlet distributed random variable.
From playlist Machine Learning

Introduction to the Dirac Delta Function
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Introduction to the Dirac Delta Function
From playlist Differential Equations

Theory of numbers: Dirichlet series
This lecture is part of an online undergraduate course on the theory of numbers. We describe the correspondence between Dirichlet series and arithmetic functions, and work out the Dirichlet series of the arithmetic functions in the previous lecture. Correction: Dave Neary pointed out t
From playlist Theory of numbers

Calderon problem (Lecture 1) by Venkateswaran P Krishnan
DISCUSSION MEETING WORKSHOP ON INVERSE PROBLEMS AND RELATED TOPICS (ONLINE) ORGANIZERS: Rakesh (University of Delaware, USA) and Venkateswaran P Krishnan (TIFR-CAM, India) DATE: 25 October 2021 to 29 October 2021 VENUE: Online This week-long program will consist of several lectures by
From playlist Workshop on Inverse Problems and Related Topics (Online)
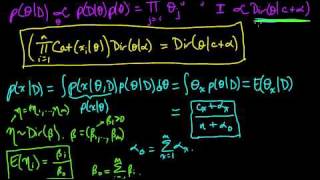
(ML 7.8) Dirichlet-Categorical model (part 2)
The Dirichlet distribution is a conjugate prior for the Categorical distribution (i.e. a PMF a finite set). We derive the posterior distribution and the (posterior) predictive distribution under this model.
From playlist Machine Learning

Topic Models: Variational Inference for Latent Dirichlet Allocation (with Xanda Schofield)
This is a single lecture from a course. If you you like the material and want more context (e.g., the lectures that came before), check out the whole course: https://sites.google.com/umd.edu/2021cl1webpage/ (Including homeworks and reading.) Xanda's Webpage: https://www.cs.hmc.edu/~xanda
From playlist Computational Linguistics I

Low moments of character sums - Adam Harper
Joint IAS/Princeton University Number Theory Seminar Topic: Low moments of character sums Speaker: Adam Harper Affiliation: University of Warwick Date: April 08, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

Calderon problem (Lecture 2) by Venkateswaran P Krishnan
DISCUSSION MEETING WORKSHOP ON INVERSE PROBLEMS AND RELATED TOPICS (ONLINE) ORGANIZERS: Rakesh (University of Delaware, USA) and Venkateswaran P Krishnan (TIFR-CAM, India) DATE: 25 October 2021 to 29 October 2021 VENUE: Online This week-long program will consist of several lectures by
From playlist Workshop on Inverse Problems and Related Topics (Online)

The Heat Equation: Lecture 4 - Oxford Mathematics 1st Year Student Lecture
The heat equation, also known as the diffusion equation, is central to many areas in applied mathematics. In this series of four lectures - this is the fourth - forming part of the first year undergraduate mathematics course, 'Fourier Series and PDEs', the heat equation is derived and the
From playlist Oxford Mathematics 1st Year Student Lectures: The Heat Equation

Introduction to number theory lecture 52. Nonvanishing of L series at s=1.
This lecture is part of my Berkeley math 115 course "Introduction to number theory" For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj53L8sMbzIhhXSAOpuZ1Fov8 We sketch how to show that Dirichlet L functions do not vanish at s=1, completing the proo
From playlist Introduction to number theory (Berkeley Math 115)

Introduction to number theory lecture 45 Dirichlet series
This lecture is part of my Berkeley math 115 course "Introduction to number theory" For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj53L8sMbzIhhXSAOpuZ1Fov8 We introduce Dirichlet series as generating functions of arithmetical functions and give so
From playlist Introduction to number theory (Berkeley Math 115)
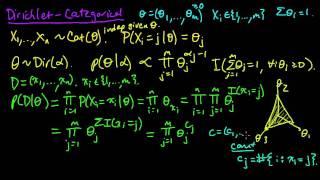
(ML 7.7) Dirichlet-Categorical model (part 1)
The Dirichlet distribution is a conjugate prior for the Categorical distribution (i.e. a PMF a finite set). We derive the posterior distribution and the (posterior) predictive distribution under this model.
From playlist Machine Learning

David Krejčiřík: Spectrum of the Möbius strip: true, fake and not-so-fake
CIRM VIRTUAL EVENT Recorded during the meeting "Shape Optimization, Spectral Geometry and Calculus of Variations" the March 30, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worl
From playlist Virtual Conference
