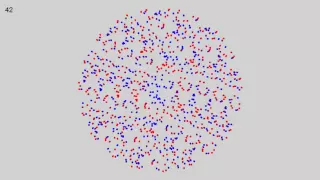
Doyle spiral
In the mathematics of circle packing, a Doyle spiral is a pattern of non-crossing circles in the plane in which each circle is surrounded by a ring of six tangent circles. These patterns contain spiral arms formed by circles linked through opposite points of tangency, with their centers on logarithmic spirals of three different shapes. Doyle spirals are named after mathematician Peter G. Doyle, who made an important contribution to their mathematical construction in the late 1980s or early 1990s. However, their study in phyllotaxis (the mathematics of plant growth) dates back to the early 20th century. (Wikipedia).