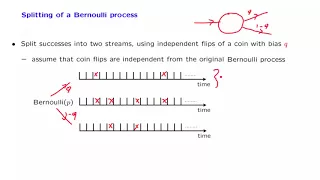
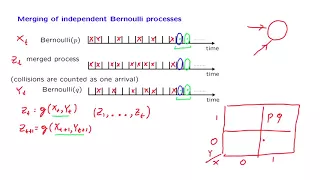
Bernoulli process
In probability and statistics, a Bernoulli process (named after Jacob Bernoulli) is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variables Xi are identically distributed and independent. Prosaically, a Bernoulli process is a repeated coin flipping, possibly with an unfair coin (but with consistent unfairness). Every variable Xi in the sequence is associated with a Bernoulli trial or experiment. They all have the same Bernoulli distribution. Much of what can be said about the Bernoulli process can also be generalized to more than two outcomes (such as the process for a six-sided die); this generalization is known as the Bernoulli scheme. The problem of determining the process, given only a limited sample of Bernoulli trials, may be called the problem of checking whether a coin is fair. (Wikipedia).