
Oblique Asymptotes (1 of 3: Comparing with other asymptotes)
More resources available at www.misterwootube.com
From playlist Further Work with Functions (related content)

Interval Notation (2 of 2: Unbounded intervals)
More resources available at www.misterwootube.com
From playlist Working with Functions

Entropy Equipartition along almost Geodesics in Negatively Curved Groups by Amos Nevo
PROGRAM : ERGODIC THEORY AND DYNAMICAL SYSTEMS (HYBRID) ORGANIZERS : C. S. Aravinda (TIFR-CAM, Bengaluru), Anish Ghosh (TIFR, Mumbai) and Riddhi Shah (JNU, New Delhi) DATE : 05 December 2022 to 16 December 2022 VENUE : Ramanujan Lecture Hall and Online The programme will have an emphasis
From playlist Ergodic Theory and Dynamical Systems 2022

Features of the Hyperbola (2 of 3: Finding the Asymptotes and Conjugate Hyperbola)
More resources available at www.misterwootube.com
From playlist Further Work with Functions (related content)

Jean-François Babadjian: On the convergence of critical points of the Ambrosio-Tortorelli functional
CONFERENCE Recorded during the meeting " Beyond Elasticity: Advances and Research Challenges " the May 19, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians
From playlist Analysis and its Applications

Entropy accumulation - O. Fawzi - Workshop 2 - CEB T3 2017
Omar Fawzi / 23.10.17 Entropy accumulation We ask the question whether entropy accumulates, in the sense that the operationally relevant total uncertainty about an n-partite system A=(A1,…An) corresponds to the sum of the entropies of its parts Ai. The Asymptotic Equipartition Property i
From playlist 2017 - T3 - Analysis in Quantum Information Theory - CEB Trimester

http://AllSignalProcessing.com for more great signal processing content, including concept/screenshot files, quizzes, MATLAB and data files. Basic properties of the z-transform: linearity, convolution, differentiation of X(z), multiplication by an exponential sequence, time-shift property
From playlist The z-Transform

What are vertical asymptotes? (KristaKingMath)
► My Applications of Derivatives course: https://www.kristakingmath.com/applications-of-derivatives-course Vertical asymptotes are important boundary lines for a function, because, if you can find them, they're a line that the graph cannot cross, which can really help you sketch a more ac
From playlist Popular Questions

Brainstorming: What is an Asymptote?
In this video, we explore what it means for a curve to have an asymptote. We focus on how to determine when a function has a vertical and/or horizontal asymptote. College Algebra homepage: http://webspace.ship.edu/jehamb/calg.html
From playlist College Algebra

When do we have an oblique, slant asymptote for a rational function
👉 Learn all about asymptotes of a rational function. A rational function is a function, having a variable in the denominator. An asymptote is a line that the graph of a function approaches but never touches. There are the vertical, the horizontal and the slant/oblique asymptotes. The ver
From playlist Asymptotes of Rational Functions | Learn About

Multi-mode Correlations in Turbulence by Gregory Falkovich
PROGRAM TURBULENCE: PROBLEMS AT THE INTERFACE OF MATHEMATICS AND PHYSICS ORGANIZERS: Uriel Frisch (Observatoire de la Côte d'Azur and CNRS, France), Konstantin Khanin (University of Toronto, Canada) and Rahul Pandit (IISc, India) DATE: 16 January 2023 to 27 January 2023 VENUE: Ramanuja
From playlist Turbulence: Problems at the Interface of Mathematics and Physics 2023

Lec 4 | MIT 6.450 Principles of Digital Communications I, Fall 2006
Lecture 4: Entropy and asymptotic equipartition property View the complete course at: http://ocw.mit.edu/6-450F06 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.450 Principles of Digital Communications, I Fall 2006

Suppression of Intermittency in the Decimated Navier-Stokes equation by Samriddhi Sankar Ray
Turbulence from Angstroms to light years DATE:20 January 2018 to 25 January 2018 VENUE:Ramanujan Lecture Hall, ICTS, Bangalore The study of turbulent fluid flow has always been of immense scientific appeal to engineers, physicists and mathematicians because it plays an important role acr
From playlist Turbulence from Angstroms to light years
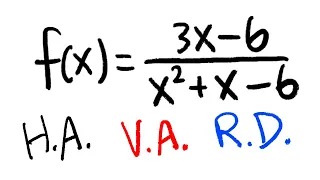
Horizontal Asymptote, Vertical Asymptote, & Removable Discontinuity
How to find the Horizontal asymptote, vertical asymptote and removable discontinuity from a rational function. #calculus For more similar examples, check out my playlist :https://www.youtube.com/playlist?list=PLb2SZv7eAqpmFSRhJAtPYis3RT2TtCWbl Horizontal Asymptote, @0:10 Vertical Asymptot
From playlist Limits at Infinities, (sect 2.6)
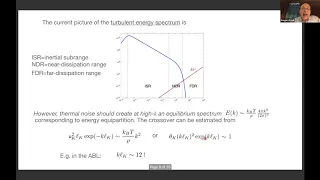
Fluid Turbulence, Thermal Noise and Spontaneous Stochasticity - Gregory Eyink
Workshop on Turbulence Topic: Fluid Turbulence, Thermal Noise and Spontaneous Stochasticity Speaker: Gregory Eyink Affiliation: Johns Hopkins University Date: December 11, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Thermodynamics and Chemical Dynamics 131C. Lecture 05. The Equipartition Theorum.
UCI Chem 131C Thermodynamics and Chemical Dynamics (Spring 2012) Lec 05. Thermodynamics and Chemical Dynamics -- The Equipartition Theorum -- View the complete course: http://ocw.uci.edu/courses/chem_131c_thermodynamics_and_chemical_dynamics.html Instructor: Reginald Penner, Ph.D. Licens
From playlist Chemistry 131C: Thermodynamics and Chemical Dynamics

Jet Formation and Propagation in FSRQs and BL Lacs by Will Potter
Extragalactic Relativistic Jets: Cause and Effect PROGRAM LINK: www.icts.res.in/program/ERG2015 DATES: Monday 12 Oct, 2015 - Tuesday 20 Oct, 2015 VENUE: Ramanujan Lecture Hall, ICTS Bangalore DESCRIPTION : Active Galactic Nuclei (AGN) are the luminous centers of galaxies that are belie
From playlist Extragalactic Relativistic Jets: Cause and Effect

Einsteins Legacy is All Around Us
Without Einstein's–and his successors'–work in quantum physics, we wouldn't have fiberoptic Internet cables, let alone technology like GPS. Smoke detectors, smartphone cameras, and the red glow in your toaster all show quantum physics at work as well. Take a look around your house with a n
From playlist Math and Statistics

How to determine if discontinuities are holes or asymptotes
👉 Learn how to find the removable and non-removable discontinuity of a function. A function is said to be discontinuous at a point when there is a gap in the graph of the function at that point. A discontinuity is said to be removable when there is a factor in the numerator which can cance
From playlist Find the Asymptotes of Rational Functions
