
Transfer Functions: Introduction and Implementation
In this video we introduce transfer functions and show how they can be derived from a set of linear, ordinary differential equations. We also examine how to use a transfer function to predict the output of system to a given input. Topics and time stamps: 0:38 – Example using an aircraft
From playlist Control Theory

What are Transfer Functions? | Control Systems in Practice
This video introduces transfer functions - a compact way of representing the relationship between the input into a system and its output. It covers why transfer functions are so popular and what they are used for. Learn more: - MATLAB Tech Talk: 4 Ways to Implement a Transfer Function in
From playlist Control Systems in Practice

Transfer operators between relative trace formulas in rank one - Yiannis Sakellaridis
Locally Symmetric Spaces Seminar Topic: Transfer operators between relative trace formulas in rank one Speaker: Yiannis Sakellaridis Affiliation: Rutgers University; von Neumann Fellow, School of Mathematics Date: December 12, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Transference is a very useful word from psychoanalysis which describes the process whereby we react to situations in the present according to a pattern laid down in the past, usually in childhood. Getting to know our own particular transferences is part of becoming a sane adult. If you lik
From playlist RELATIONSHIPS

Electrical Engineering: Ch 15: Frequency Response (1 of 56) What is a Transfer Function? 1 of 3
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is a transfer function – the frequency dependent ratio (represented by a number between 0 and 1) of the output vs input voltage (or current). http://www.ilectureonline.com/donate https:/
From playlist ELECTRICAL ENGINEERING 15 FREQUENCY RESPONSE
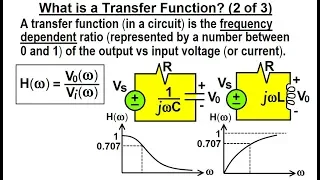
Electrical Engineering: Ch 15: Frequency Response (2 of 56) What is a Transfer Function? 2 of 3
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is a transfer function using simple circuits and how it is associated with the transfer function which is frequency dependent. http://www.ilectureonline.com/donate https://www.patreon.co
From playlist ELECTRICAL ENGINEERING 15 FREQUENCY RESPONSE

Transfer operator approach to 1d random band matrices – Mariya Shcherbina – ICM2018
Mathematical Physics Invited Lecture 11.7 Transfer operator approach to 1d random band matrices Mariya Shcherbina Abstract: We discuss an application of the transfer operator approach to the analysis of the different spectral characteristics of 1d random band matrices (correlation functi
From playlist Mathematical Physics

Oscar Bandtlow: Spectral approximation of transfer operators
The lecture was held within the framework of the Hausdorff Trimester Program "Dynamics: Topology and Numbers": Conference on “Transfer operators in number theory and quantum chaos” Abstract:The talk will be concerned with the problem of how to approximate spectral data oftra
From playlist Conference: Transfer operators in number theory and quantum chaos

Transfer operators between relative trace formulas in rank one II - Yiannis Sakellaridis
Locally Symmetric Spaces Seminar Topic: Transfer operators between relative trace formulas in rank one II Speaker: Yiannis Sakellaridis Affiliation: Rutgers University; von Neumann Fellow, School of Mathematics Date: December 19, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

MIT Electronic Feedback Systems (1985) View the complete course: http://ocw.mit.edu/RES6-010S13 Instructor: James K. Roberge License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT Electronic Feedback Systems (1985)

Inner Functions Revisited by Jon Aaronson
PROGRAM : ERGODIC THEORY AND DYNAMICAL SYSTEMS (HYBRID) ORGANIZERS : C. S. Aravinda (TIFR-CAM, Bengaluru), Anish Ghosh (TIFR, Mumbai) and Riddhi Shah (JNU, New Delhi) DATE : 05 December 2022 to 16 December 2022 VENUE : Ramanujan Lecture Hall and Online The programme will have an emphasis
From playlist Ergodic Theory and Dynamical Systems 2022

Basic Lectures on Bethe Ansatz (Pedagogical Lecture 03) by Fabio Franchini
PROGRAM: INTEGRABLE SYSTEMS IN MATHEMATICS, CONDENSED MATTER AND STATISTICAL PHYSICS ORGANIZERS: Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE : 16 July 2018 to 10 August 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

Matteo Tanzi - Self-consistent transfer operators for high-dimensional expanding coupled maps
Recorded 29 August 2022. Matteo Tanzi of New York University presents "Self-consistent transfer operators for high-dimensional expanding coupled maps" at IPAM's Reconstructing Network Dynamics from Data: Applications to Neuroscience and Beyond. Abstract: Recently, much progress has been ma
From playlist 2022 Reconstructing Network Dynamics from Data: Applications to Neuroscience and Beyond

13. Operational Amplifier Compensation (continued)
MIT Electronic Feedback Systems (1985) View the complete course: http://ocw.mit.edu/RES6-010S13 Instructor: James K. Roberge License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT Electronic Feedback Systems (1985)

Tobias Weich: Resonance chains on Schottky surfaces
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist SPECIAL 7th European congress of Mathematics Berlin 2016.

Yiannis Sakellaridis - 1/2 Local and Global Questions “Beyond Endoscopy”
The near-completion of the program of endoscopy poses the question of what lies next. These talks will take a broad view of ideas beyond the program of endoscopy, highlighting the connections among them, and emphasizing the relationship between local and global aspects. Central among thos
From playlist 2022 Summer School on the Langlands program

The appearance of noise like behaviour (...) systems - CEB T2 2017 - Liverani - 2/3
Carlangelo Liverani (Univ. Roma Tor Vergata) - 30/05/17 The appearance of noise like behaviour in deterministic dynamical systems I will discuss how noise can arise in deterministic systems with strong instability with respect to the initial conditions. Starting with a discussion of the C
From playlist 2017 - T2 - Stochastic Dynamics out of Equilibrium - CEB Trimester

Non-Hermitian Hamiltonians and Low-Energy Scattering in one Dimension by Ali Mostafazadeh
PROGRAM NON-HERMITIAN PHYSICS (ONLINE) ORGANIZERS: Manas Kulkarni (ICTS, India) and Bhabani Prasad Mandal (Banaras Hindu University, India) DATE: 22 March 2021 to 26 March 2021 VENUE: Online Non-Hermitian Systems / Open Quantum Systems are not only of fundamental interest in physics a
From playlist Non-Hermitian Physics (ONLINE)

MIT Electronic Feedback Systems (1985) View the complete course: http://ocw.mit.edu/RES6-010S13 Instructor: James K. Roberge License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT Electronic Feedback Systems (1985)

Ever heard of Quantum Operators and Commutators? (Explained for Beginners)!
What is a quantum operator? And just how useful are quantum commutators? Find out how they help us understand the Ehrenfest Theorem! Hi everyone, I'm back with a new video! This time it's the first in a two-part mini-series on one of the coolest theorems in quantum mechanics - Ehrenfest's
From playlist Quantum Physics by Parth G