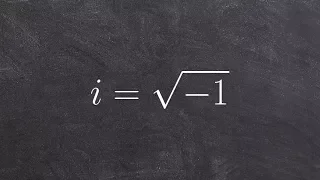Algebraic numbers | Euclidean plane geometry
Constructible number
In geometry and algebra, a real number is constructible if and only if, given a line segment of unit length, a line segment of length can be constructed with compass and straightedge in a finite number of steps. Equivalently, is constructible if and only if there is a closed-form expression for using only integers and the operations for addition, subtraction, multiplication, division, and square roots. The geometric definition of constructible numbers motivates a corresponding definition of constructible points, which can again be described either geometrically or algebraically. A point is constructible if it can be produced as one of the points of a compass and straight edge construction (an endpoint of a line segment or crossing point of two lines or circles), starting from a given unit length segment. Alternatively and equivalently, taking the two endpoints of the given segment to be the points (0, 0) and (1, 0) of a Cartesian coordinate system, a point is constructible if and only if its Cartesian coordinates are both constructible numbers. Constructible numbers and points have also been called ruler and compass numbers and ruler and compass points, to distinguish them from numbers and points that may be constructed using other processes. The set of constructible numbers forms a field: applying any of the four basic arithmetic operations to members of this set produces another constructible number. This field is a field extension of the rational numbers and in turn is contained in the field of algebraic numbers. It is the Euclidean closure of the rational numbers, the smallest field extension of the rationals that includes the square roots of all of its positive numbers. The proof of the equivalence between the algebraic and geometric definitions of constructible numbers has the effect of transforming geometric questions about compass and straightedge constructions into algebra, including several famous problems from ancient Greek mathematics. The algebraic formulation of these questions led to proofs that their solutions are not constructible, after the geometric formulation of the same problems previously defied centuries of attack. (Wikipedia).