
Number theory Full Course [A to Z]
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure #mathematics devoted primarily to the study of the integers and integer-valued functions. Number theorists study prime numbers as well as the properties of objects made out of integers (for example, ratio
From playlist Number Theory
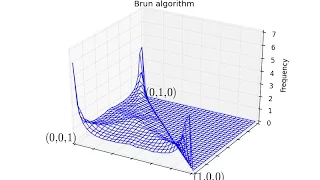
Analytic Number Theory with Sage - Kamalakshya Mehatab
Video taken from: http://ekalavya.imsc.res.in/node/451
From playlist Mathematics

Factorials, prime numbers, and the Riemann Hypothesis
Today we introduce some of the ideas of analytic number theory, and employ them to help us understand the size of n!. We use that understanding to discover a surprisingly accurate picture of the distribution of the prime numbers, and explore how this fits into the broader context of one o
From playlist Analytic Number Theory

Determine Rational or Irrational Numbers (Square Roots and Decimals Only)
This video explains how to determine if a given number is rational or irrational.
From playlist Functions

Set Theory (Part 14a): Constructing the Complex Numbers
Please leave your thoughts and questions below! In this video, we will extend the real numbers to the complex numbers and investigate the algebraic structure of the complex numbers after defining addition and multiplication of these new objects. We will also begin to see how complex numbe
From playlist Set Theory by Mathoma

Field Definition (expanded) - Abstract Algebra
The field is one of the key objects you will learn about in abstract algebra. Fields generalize the real numbers and complex numbers. They are sets with two operations that come with all the features you could wish for: commutativity, inverses, identities, associativity, and more. They
From playlist Abstract Algebra

Theory of numbers: Multiplicative functions
This lecture is part of an online undergraduate course on the theory of numbers. Multiplicative functions are functions such that f(mn)=f(m)f(n) whenever m and n are coprime. We discuss some examples, such as the number of divisors, the sum of the divisors, and Euler's totient function.
From playlist Theory of numbers

Philosophy of Mathematics & Frege (Dummett 1994)
Michael Dummett gives a talk on Frege and the philosophy of mathematics. For a good introduction to the philosophy of mathematics, check out: https://www.youtube.com/watch?v=UhX1ouUjDHE Another good introduction to the philosophy of mathematics: https://www.youtube.com/watch?v=XyXWnGFKTkg
From playlist Logic & Philosophy of Mathematics

Intro to the Philosophy of Mathematics (Ray Monk)
A good introduction to the philosophy of mathematics by Ray Monk. He considers the issue of the nature of mathematical truth - what mathematics is actually about - and discusses the views of Plato, Aristotle, Kant, Frege and Russell. What is mathematics about? Is mathematics something disc
From playlist Logic & Philosophy of Mathematics

Peter Sarnak: Hyperbolic equations and spectral geometry
Programme for the Abel Lectures 2005: 1. "Abstract Phragmen-Lindelöf theorem & Saint Venant’s principle" by Abel Laureate 2005 Peter D. Lax, New York University 2. "Systems of conservation laws" by Professor Sebastian Noelle, CMA Oslo/ RWTH Aachen 3. "Hyperbolic equations and spectra
From playlist Abel Lectures

Recent progress in multiplicative number theory – Kaisa Matomäki & Maksym Radziwiłł – ICM2018
Number Theory Invited Lecture 3.5 Recent progress in multiplicative number theory Kaisa Matomäki & Maksym Radziwiłł Abstract: Multiplicative number theory aims to understand the ways in which integers factorize, and the distribution of integers with special multiplicative properties (suc
From playlist Number Theory

Complex Variables by Francis J. Flanigan
This is Complex Variables by Francis Flanigan. This math book is pretty good all around. It's also very affordable as it is a paperback reprint by Dover. Here it is https://amzn.to/3mIJQiq Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear https://amzn.to/3BFvcxp (these are my
From playlist Book Reviews

Thoughts, Thinking, & Thinkers (Tim Crane - 2017 Frege Lectures)
Professor Tim Crane gives a series of talks called "Thoughts, Thinking, & Thinkers" as part of the 2017 Frege Lectures in theoretical philosophy at the University of Tartu. Note, this is a re-upload. One of Frege’s most famous principles was ‘always to separate sharply the psychological
From playlist Philosophy of Mind

Mod-01 Lec-01 Introduction and Overview
Advanced Numerical Analysis by Prof. Sachin C. Patwardhan,Department of Chemical Engineering,IIT Bombay.For more details on NPTEL visit http://nptel.ac.in
From playlist IIT Bombay: Advanced Numerical Analysis | CosmoLearning.org

SHM - 16/01/15 - Constructivismes en mathématiques - Frédéric Brechenmacher
Frédéric Brechenmacher (LinX, École polytechnique), « Effectivité et généralité dans la construction des grandeurs algébriques de Kronecker »
From playlist Les constructivismes mathématiques - Séminaire d'Histoire des Mathématiques

Analytic Continuation and the Zeta Function
Where do complex functions come from? In this video we explore the idea of analytic continuation, a powerful technique which allows us to extend functions such as sin(x) from the real numbers into the complex plane. Using analytic continuation we can finally define the zeta function for co
From playlist Analytic Number Theory
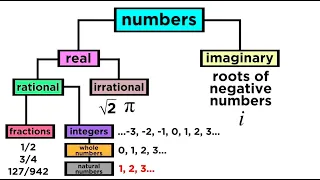
What are the Types of Numbers? Real vs. Imaginary, Rational vs. Irrational
We've mentioned in passing some different ways to classify numbers, like rational, irrational, real, imaginary, integers, fractions, and more. If this is confusing, then take a look at this handy-dandy guide to the taxonomy of numbers! It turns out we can use a hierarchical scheme just lik
From playlist Algebra 1 & 2
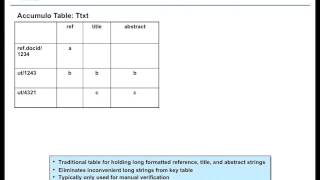
RES.LL-005 D4M: Signal Processing on Databases, Fall 2012 View the complete course: http://ocw.mit.edu/RESLL-005F12 Instructor: Jeremy Kepner Creating an exploded database schema. Standard database processing chain. Graph adjacency matrix. Vertex degree distribution. Directed graphs, mu
From playlist MIT D4M: Signal Processing on Databases, Fall 2012

