
What is an Injective Function? Definition and Explanation
An explanation to help understand what it means for a function to be injective, also known as one-to-one. The definition of an injection leads us to some important properties of injective functions! Subscribe to see more new math videos! Music: OcularNebula - The Lopez
From playlist Functions
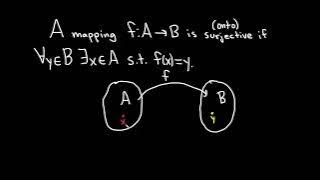
Definition of a Surjective Function and a Function that is NOT Surjective
We define what it means for a function to be surjective and explain the intuition behind the definition. We then do an example where we show a function is not surjective. Surjective functions are also called onto functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear ht
From playlist Injective, Surjective, and Bijective Functions

Definition of an Injective Function and Sample Proof
We define what it means for a function to be injective and do a simple proof where we show a specific function is injective. Injective functions are also called one-to-one functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear https://amzn.to/3BFvcxp (these are my affil
From playlist Injective, Surjective, and Bijective Functions

The Definition of a Surjective(Onto) Function and Explanation
The Definition of a Surjective(Onto) Function and Explanation
From playlist Functions, Sets, and Relations
Lecture 5: The definition of a topos (Part 2)
A topos is a Cartesian closed category with all finite limits and a subobject classifier. In his two seminar talks (of which this is the second) James Clift will explain all of these terms in detail. In his first talk he defined products, pullbacks, general limits, and exponentials and in
From playlist Topos theory seminar

Lecture 4: The definition of a topos (Part 1)
A topos is a Cartesian closed category with all finite limits and a subobject classifier. In his two seminar talks (of which this is the first) James Clift will explain all of these terms in detail. In this talk he defines products, pullbacks, general limits, and exponentials and in Part 2
From playlist Topos theory seminar

Topoi 2: The Subobject Classifier diagram
Topos, topoi, toposes. Previous video 1: https://youtu.be/Ysp7P4wW-zE This is the second video, discussing of the Subobject Classifier in a category of sets. For the followup video, just look at the videos uploaded one, two weeks later. The document used can be found here: https://gist.gi
From playlist Logic

AlgTopReview: An informal introduction to abstract algebra
This is a review lecture on some aspects of abstract algebra useful for algebraic topology. It provides some background on fields, rings and vector spaces for those of you who have not studied these objects before, and perhaps gives an overview for those of you who have. Our treatment is
From playlist Algebraic Topology

Eleftherios Pavlides & Thomas Banchoff - Hinge Elastegrities Shape Shifting - G4G12 April 2016
Named by analogy to tensegrity, maintaining form integrity through tension alone, hinge-elastegrity, maintaining form integrity with elastic hinges, is created by folding and weaving a shape-memory membrane, into a network of rigid members suspended with elastic hinges. The shape-shifting
From playlist G4G12 Videos
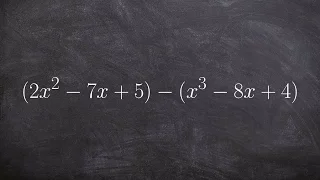
Subtracting polynomials by using the addition method
👉 Learn how to subtract polynomials. To subtract polynomials, we first simplify the polynomials by removing all brackets. Then, we combine like terms. Like terms are terms that share the same base and power for each variable. When you have identified the like terms, we then apply the requ
From playlist How to subtract polynomials

👉 Learn how to subtract polynomials. To subtract polynomials, we first simplify the polynomials by removing all brackets. Then, we combine like terms. Like terms are terms that share the same base and power for each variable. When you have identified the like terms, we then apply the requ
From playlist How to subtract polynomials

👉 Learn how to subtract polynomials. To subtract polynomials, we first simplify the polynomials by removing all brackets. Then, we combine like terms. Like terms are terms that share the same base and power for each variable. When you have identified the like terms, we then apply the requ
From playlist How to subtract polynomials

Subtracting linear functions to find domain
👉 Learn how to add or subtract two functions. Given two functions, say f(x) and g(x), to add (f+g)(x) or f(x) + g(x) or to subtract (f - g)(x) or f(x) - g(x) the two functions we use the method of adding/subtracting algebraic expressions together. To add or subtract two linear functions, w
From playlist Add and Subtract Functions

Lecture 11: Sheaves form a topos (Part 2)
In this talk Patrick Elliott proves that the category of sheaves on a site is a topos, by discussing the exponentials and subobject classifier in detail. The notes are already online: The lecture notes are available here: http://therisingsea.org/notes/ch2018-lecture11.pdf. For the genera
From playlist Topos theory seminar

Lecture 13: Higher-order logic and topoi (Part 3)
In this talk James Clift explains how to think about quantifiers in the context of topoi using adjunctions, and more generally how to extract a type theory out of a topos. This provides the means to "cut out" subobjects using formulas, which is in turn the fundamental idea to defining clas
From playlist Topos theory seminar

Intro to Subsequences | Real Analysis
What are subsequences in real analysis? In today's lesson we'll define subsequences, and see examples and nonexamples of subsequences. We can learn a lot about a sequence by studying its subsequence, so let's talk about it! If (a_n) is a sequence, we can denote a subsequence of (a_n) as (
From playlist Real Analysis

The Composition of Surjective(Onto) Functions is Surjective Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys The Composition of Surjective(Onto) Functions is Surjective Proof. I included some pictures in the proof with the hope that perhaps it makes more sense.
From playlist Proofs
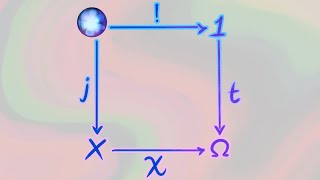
Topoi 1: Predicates vs. subsets
Topos, topoi, toposes. This is the warmup video for the discussion of the Subobject Classifier in a category of sets, in the next video. The document used can be found here: https://gist.github.com/Nikolaj-K/469b9ca1c085ea4ac4e3d7d0008913f5 Typo: In minute 42, the membership relation on sh
From playlist Logic