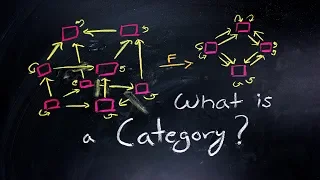
Categories for the Working Mathematician (CWM) is a textbook in category theory written by American mathematician Saunders Mac Lane, who cofounded the subject together with Samuel Eilenberg. It was first published in 1971, and is based on his lectures on the subject given at the University of Chicago, the Australian National University, Bowdoin College, and Tulane University. It is widely regarded as the premier introduction to the subject. (Wikipedia).
This lecture is part of an online course on Category theory This is the introductory lecture, where we give a few examples of categories and define them. The lectures were originally part of a graduate algebra course, and give a quick overview of the basic category theory that is useful
From playlist Categories for the idle mathematician
What is a Category? | Nathan Dalaklis
Categories and Functors can be pretty mindboggling mathematical objects to wrap your head around if you're not used to abstract math, but they come up as useful tools to study different structures in mathematics and beyond. So... What is a Category? Here I introduce the definition of a Cat
From playlist The New CHALKboard
What are the Types of Numbers? Real vs. Imaginary, Rational vs. Irrational
We've mentioned in passing some different ways to classify numbers, like rational, irrational, real, imaginary, integers, fractions, and more. If this is confusing, then take a look at this handy-dandy guide to the taxonomy of numbers! It turns out we can use a hierarchical scheme just lik
From playlist Algebra 1 & 2
Recommended books for the undergrad category theorist
I'll talk more about universal constructions on this channel, so best subscribe. In this video I go through a curated list of introductory text about category theory. You can find the list here: https://gist.github.com/Nikolaj-K/282515e58c1c14de2e25222065f77a0a In the video I comment on a
From playlist Algebra
SketchySVD - Joel Tropp, California Institute of Technology
This workshop - organised under the auspices of the Isaac Newton Institute on “Approximation, sampling and compression in data science” — brings together leading researchers in the general fields of mathematics, statistics, computer science and engineering. About the event The workshop ai
From playlist Mathematics of data: Structured representations for sensing, approximation and learning
Classification of Real Numbers, Inequalities, and Number Line
I define and discuss Real Numbers their subsets of Rational Numbers, Integers, Whole Numbers, Natural Numbers, and finally Irrational Numbers. I finish with Inequalities and the Number line at 23:53 Find free review test, useful notes and more at http://www.mathplane.com If you'd like to
From playlist Algebra 1
This lecture is part of an online course on category theory. We define functors and give some examples of them. For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj51F9XZ_Ka4bLnQoxTdMx0AL
From playlist Categories for the idle mathematician
Sets and other data structures | Data Structures in Mathematics Math Foundations 151
In mathematics we often want to organize objects. Sets are not the only way of doing this: there are other data types that are also useful and that can be considered together with set theory. In particular when we group objects together, there are two fundamental questions that naturally a
From playlist Math Foundations
The Woman Who's Rewriting Higher Category Theory
By turning higher category theory on itself, Emily Riehl hopes to make the powerful perspective more accessible to other mathematicians. Read the full interview here: https://www.quantamagazine.org/emily-riehl-conducts-the-mathematical-orchestra-from-the-middle-20200902/ 0:00 What is cate
From playlist Inside the Mind of a Scientist
Huawei Young Talents Programme - Laurent Lafforgue
The online ceremony celebrating the official launch of the Huawei Young Talents Program at the Institut des Hautes Etudes Scientifiques was held on 6 November 2020. This program aims to support the work of talented researchers in mathematics and theoretical physics at the beginning of thei
From playlist Huawei Young Talents Program - November 2020
Adam Topaz - The Liquid Tensor Experiment - IPAM at UCLA
Recorded 13 February 2023. Adam Topaz of the University of Alberta presents "The Liquid Tensor Experiment" at IPAM's Machine Assisted Proofs Workshop. Learn more online at: http://www.ipam.ucla.edu/programs/workshops/machine-assisted-proofs/
From playlist 2023 Machine Assisted Proofs Workshop
Math Talk! Dr. Andrej Bauer on proof assistants, constructive mathematics, philosophy, and more.
In this wonderful discussion with Dr. Andrej Bauer we discuss a whole host of topics centering around constructive mathematics, and proof assistants. Support Ukraine through Shtab Dobra: Instagram: https://www.instagram.com/shtab.dobra/ Facebook: https://www.facebook.com/shtab.dobra PayPa
From playlist Math Talk!
Twisted S-duality by Philsang Yoo
PROGRAM QUANTUM FIELDS, GEOMETRY AND REPRESENTATION THEORY 2021 (ONLINE) ORGANIZERS: Aswin Balasubramanian (Rutgers University, USA), Indranil Biswas (TIFR, india), Jacques Distler (The University of Texas at Austin, USA), Chris Elliott (University of Massachusetts, USA) and Pranav Pan
From playlist Quantum Fields, Geometry and Representation Theory 2021 (ONLINE)
Galois, Grothendieck and Voevodsky - George Shabat
Vladimir Voevodsky Memorial Conference Topic: Galois, Grothendieck and Voevodsky Speaker: George Shabat Affiliation: Russian State University for the Humanities Date: September 12, 2018 For more video please visit http://video.ias.edu
From playlist Vladimir Voevodsky Memorial Conference
Tai-Danae Bradley: Where math meets language | 3b1b Podcast #5
Tai-Danae Bradley does research applying tools from physics to understanding language models, all under the broader umbrella of category theory. She is also the brilliant mind behind the blog https://www.math3ma.com/ Try out the episode sponsor: http://brilliant.org/3b1b Guide to Tai-D
From playlist 3b1b Podcast (reverse order)
ICM 2018 - Rio de Janeiro | http://www.icm2018.org © 2018 Rio ICM2018 & International Mathematical Union Os direitos sobre todo o material deste canal pertencem ao Instituto de Matemática Pura e Aplicada, sendo vedada a utilização total ou parcial do conteúdo sem autorização prévia e
From playlist Ceremonies ICM 2018
Math Talk! Dr. Emily Riehl, to infinity categories and beyond.
In this video I have a lovely discussion with Dr. Emily Riehl about math, HoTT, infinity categories, and more! Dr. Riehl's site, with links to publications: https://emilyriehl.github.io/ Dr. Riehl's band, Unstraight: https://unstraightmusic.com/ Spectra: http://lgbtmath.org/
From playlist Math Talk!
The Practice of Mathematics - Part 11
The Practice of Mathematics Ropert P. Langlands Institute for Advanced Study February 15, 2000 Robert P. Langlands, Professor Emeritus, School of Mathematics. There are several central mathematical problems, or complexes of problems, that every mathematician who is eager to acquire some
From playlist Mathematics
