Objects (category theory) | Topos theory
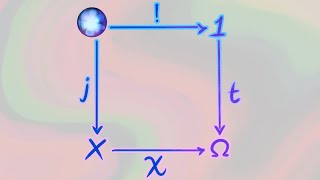
Subobject classifier
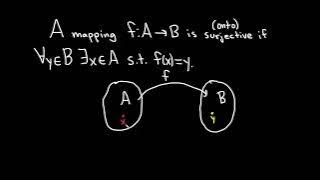
In category theory, a subobject classifier is a special object Ω of a category such that, intuitively, the subobjects of any object X in the category correspond to the morphisms from X to Ω. In typical examples, that morphism assigns "true" to the elements of the subobject and "false" to the other elements of X. Therefore, a subobject classifier is also known as a "truth value object" and the concept is widely used in the categorical description of logic. Note however that subobject classifiers are often much more complicated than the simple binary logic truth values {true, false}. (Wikipedia).