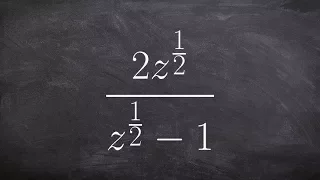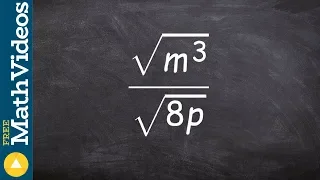Renormalization
Renormalization is a collection of techniques in quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, that are used to treat infinities arising in calculated quantities by altering values of these quantities to compensate for effects of their self-interactions. But even if no infinities arose in loop diagrams in quantum field theory, it could be shown that it would be necessary to renormalize the mass and fields appearing in the original Lagrangian. For example, an electron theory may begin by postulating an electron with an initial mass and charge. In quantum field theory a cloud of virtual particles, such as photons, positrons, and others surrounds and interacts with the initial electron. Accounting for the interactions of the surrounding particles (e.g. collisions at different energies) shows that the electron-system behaves as if it had a different mass and charge than initially postulated. Renormalization, in this example, mathematically replaces the initially postulated mass and charge of an electron with the experimentally observed mass and charge. Mathematics and experiments prove that positrons and more massive particles like protons exhibit precisely the same observed charge as the electron – even in the presence of much stronger interactions and more intense clouds of virtual particles. Renormalization specifies relationships between parameters in the theory when parameters describing large distance scales differ from parameters describing small distance scales. Physically, the pileup of contributions from an infinity of scales involved in a problem may then result in further infinities. When describing spacetime as a continuum, certain statistical and quantum mechanical constructions are not well-defined. To define them, or make them unambiguous, a continuum limit must carefully remove "construction scaffolding" of lattices at various scales. Renormalization procedures are based on the requirement that certain physical quantities (such as the mass and charge of an electron) equal observed (experimental) values. That is, the experimental value of the physical quantity yields practical applications, but due to their empirical nature the observed measurement represents areas of quantum field theory that require deeper derivation from theoretical bases. Renormalization was first developed in quantum electrodynamics (QED) to make sense of infinite integrals in perturbation theory. Initially viewed as a suspect provisional procedure even by some of its originators, renormalization eventually was embraced as an important and self-consistent actual mechanism of scale physics in several fields of physics and mathematics. Today, the point of view has shifted: on the basis of the breakthrough renormalization group insights of Nikolay Bogolyubov and Kenneth Wilson, the focus is on variation of physical quantities across contiguous scales, while distant scales are related to each other through "effective" descriptions. All scales are linked in a broadly systematic way, and the actual physics pertinent to each is extracted with the suitable specific computational techniques appropriate for each. Wilson clarified which variables of a system are crucial and which are redundant. Renormalization is distinct from regularization, another technique to control infinities by assuming the existence of new unknown physics at new scales. (Wikipedia).
