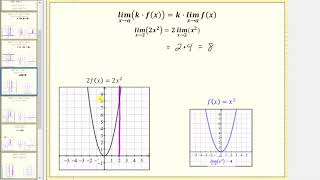
This video covers the properties of limits and verifies them graphically.
From playlist Limits
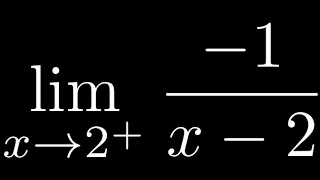
How to Compute a One Sided limit as x approaches from the right
In this video I will show you How to Compute a One Sided limit as x approaches from the right.
From playlist One-sided Limits

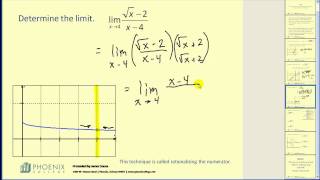
Determine Limits Using Limit Laws (Properties)
This video explains how to determine limits using limit laws or limit properties.
From playlist Limits
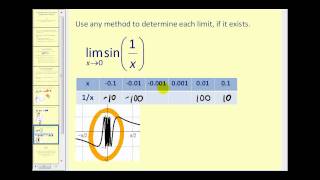
Determining Limits of Trigonometric Functions
An introductory video on determining limits of trigonometric functions. http://mathispower4u.wordpress.com/
From playlist Limits

Calculus 2.4 The Precise Definition of a Limit
My notes are available at http://asherbroberts.com/ (so you can write along with me). Calculus: Early Transcendentals 8th Edition by James Stewart
From playlist Calculus

Computing Limits from a Graph with Infinities
In this video I do an example of computing limits from a graph with infinities.
From playlist Limits

Examples 2: Determining Limits and One-Sided Limits Graphically
This video provides several examples of determining limits and one-sided limits graphically. Complete Video List at http://www.mathispower4u.com
From playlist Limits

Calculus 2.1b - Intro to Limits
continued from the previous video. An introduction to the chapter on Limits.
From playlist Calculus Chapter 2: Limits (Complete chapter)

Rita Ferreira: "Homogenization of a stationary mean-field game via two-scale convergence"
High Dimensional Hamilton-Jacobi PDEs 2020 Workshop III: Mean Field Games and Applications "Homogenization of a stationary mean-field game via two-scale convergence" Rita Ferreira - King Abdullah Univ. of Science and Technology (KAUST) Abstract: In this talk, we address the study of the
From playlist High Dimensional Hamilton-Jacobi PDEs 2020

C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 2
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with uniform lower bounds on their scalar curvature. We close the course by presenting methods and the
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Diffusion from deterministic dynamics - Antti Kupiainen
Antti Kupiainen University of Helsinki; Member, School of Mathematics October 24, 2013 I discuss a renormalization group method to derive diffusion from time reversible quantum or classical microscopic dynamics. I start with the problem of return to equilibrium and derivation of Brownian m
From playlist Mathematics

Diffusion from deterministic dynamics - Antti Kupiainen
Antti Kupiainen University of Helsinki; Member, School of Mathematics October 24, 2013 I discuss a renormalization group method to derive diffusion from time reversible quantum or classical microscopic dynamics. I start with the problem of return to equilibrium and derivation of Brownian m
From playlist Mathematics

C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 2 (version temporaire)
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with uniform lower bounds on their scalar curvature. We close the course by presenting methods and the
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Martin Hairer (DDMCS@Turing): Universality classes for 1+1 dimensional systems
Complex models in all areas of science and engineering, and in the social sciences, must be reduced to a relatively small number of variables for practical computation and accurate prediction. In general, it is difficult to identify and parameterize the crucial features that must be incorp
From playlist Data driven modelling of complex systems

Constructing a solution of the 2D Kardar-Parisi-Zhang equation (Lecture - 03) by Sourav Chatterjee
INFOSYS-ICTS RAMANUJAN LECTURES SOME OPEN QUESTIONS ABOUT SCALING LIMITS IN PROBABILITY THEORY SPEAKER Sourav Chatterjee (Stanford University, California, USA) DATE & TIME 14 January 2019 to 18 January 2019 VENUE Madhava Lecture Hall, ICTS campus GALLERY Lecture 1: Yang-Mills for mathemat
From playlist Infosys-ICTS Ramanujan Lectures

Martin Hairer: Survey of research directions
SMRI-MATRIX Symposium with Martin Hairer 4 February 2021: Survey of research directions Title: Open problems and conjectures in SPDE theory Abstract: We will survey a number of open problems and conjectures both within SPDE theory and linking SPDE theory to other areas of mathematics.
From playlist Symposium with Martin Hairer

Anomalous Collective Diffusion of Interacting Self-propelled Particles by Punyabrata Pradhan
DISCUSSION MEETING : STATISTICAL PHYSICS OF COMPLEX SYSTEMS ORGANIZERS : Sumedha (NISER, India), Abhishek Dhar (ICTS-TIFR, India), Satya Majumdar (University of Paris-Saclay, France), R Rajesh (IMSc, India), Sanjib Sabhapandit (RRI, India) and Tridib Sadhu (TIFR, India) DATE : 19 December
From playlist Statistical Physics of Complex Systems - 2022

Jens Marklof - Quantum Lorentz gas in the Boltzmann-Grad limit: random vs periodic
Jens Marklof (University of Bristol) Quantum Lorentz gas in the Boltzmann-Grad limit: random vs periodic. A major challenge in the kinetic theory of gases is to establish the convergence of the dynamics to a macroscopic transport process described by the appropriate kinetic equation. In
From playlist Large-scale limits of interacting particle systems

Part 1: Formal Definition of a Limit
This video states the formal definition of a limit and provide an epsilon delta proof that a limit exists. complete Video Library at http://www.mathispower4u.com
From playlist Limits