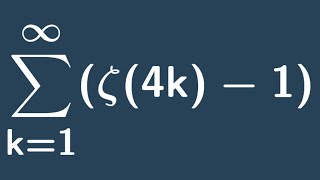In mathematics, the Hurwitz zeta function is one of the many zeta functions. It is formally defined for complex variables s with Re(s) > 1 and a ≠ 0, −1, −2, … by This series is absolutely convergent for the given values of s and a and can be extended to a meromorphic function defined for all s ≠ 1. The Riemann zeta function is ζ(s,1). The Hurwitz zeta function is named after Adolf Hurwitz, who introduced it in 1882. (Wikipedia).
More identities involving the Riemann-Zeta function!
By applying some combinatorial tricks to an identity from https://youtu.be/2W2Ghi9idxM we are able to derive two identities involving the Riemann-Zeta function. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function
Some identities involving the Riemann-Zeta function.
After introducing the Riemann-Zeta function we derive a generating function for its values at positive even integers. This generating function is used to prove two sum identities. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function
Monotonicity of the Riemann zeta function and related functions - P Zvengrowski [2012]
General Mathematics Seminar of the St. Petersburg Division of Steklov Institute of Mathematics, Russian Academy of Sciences May 17, 2012 14:00, St. Petersburg, POMI, room 311 (27 Fontanka) Monotonicity of the Riemann zeta function and related functions P. Zvengrowski University o
From playlist Number Theory
Understanding and computing the Riemann zeta function
In this video I explain Riemann's zeta function and the Riemann hypothesis. I also implement and algorithm to compute the return values - here's the Python script:https://gist.github.com/Nikolaj-K/996dba1ff1045d767b10d4d07b1b032f
From playlist Programming
Weil conjectures 1 Introduction
This talk is the first of a series of talks on the Weil conejctures. We recall properties of the Riemann zeta function, and describe how Artin used these to motivate the definition of the zeta function of a curve over a finite field. We then describe Weil's generalization of this to varie
From playlist Algebraic geometry: extra topics
Jeremy Booher, Can you hear the shape of a curve
VaNTAGe seminar, on Nov 24, 2020 License: CC-BY-NC-SA.
From playlist ICERM/AGNTC workshop updates
David Zureick-Brown, Moduli spaces and arithmetic statistics
VaNTAGe seminar on March 3, 2020 License: CC-BY-NC-SA Closed captions provided by Andrew Sutherland.
From playlist Class groups of number fields
Maxim Kazarian - 3/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants
Maxim Kazarian - 2/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants
Maxim Kazarian - 1/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants
Algebraic geometry 46: Examples of Hurwitz curves
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It gives examples of complex curves of genus 2 and 3 with the largest possible symmetry groups .
From playlist Algebraic geometry I: Varieties
Revisiting the BASEL PROBLEM: Double Integral Representation on the Unit Square!
Help me create more free content! =) https://www.patreon.com/mathable Merch :v - https://teespring.com/de/stores/papaflammy https://shop.spreadshirt.de/papaflammy 2nd Channel: https://www.youtube.com/channel/UCPctvztDTC3qYa2amc8eTrg Basel Problem: https://youtu.be/MAoI
From playlist Integrals
The most FUN Series I EVER Evaluated! An Analytic Number Theory EXTRAVAGANZA!
Help me create more free content! =) https://www.patreon.com/mathable Merch :v - https://teespring.com/de/stores/papaflammy https://www.amazon.com/shop/flammablemaths https://shop.spreadshirt.de/papaflammy Outtakes: https://youtu.be/Fjnkciqu-Cw Polygam
From playlist Integrals
Akshay Venkatesh's Fields Medal Laudatio — Peter Sarnak — ICM2018
The work of Akshay Venkatesh Peter Sarnak ICM 2018 - International Congress of Mathematicians © www.icm2018.org Os direitos sobre todo o material deste canal pertencem ao Instituto de Matemática Pura e Aplicada, sendo vedada a utilização total ou parcial do conteúdo sem autorização pr
From playlist Special / Prizes Lectures
Dimitri Zvonkine - Hurwitz numbers, the ELSV formula, and the topological recursion
We will use the example of Hurwitz numbers to make an introduction into the intersection theory of moduli spaces of curves and into the subject of topological recursion.
From playlist Physique mathématique des nombres de Hurwitz pour débutants
Niebur Integrals and Mock Automorphic Forms - Wladimir de Azevedo Pribitkin
Wladimir de Azevedo Pribitkin College of Staten Island, CUNY March 17, 2011 Among the bounty of brilliancies bequeathed to humanity by Srinivasa Ramanujan, the circle method and the notion of mock theta functions strike wonder and spark intrigue in number theorists fresh and seasoned alike
From playlist Mathematics
Arthur Krener: "Al'brekht’s Method in Infinite Dimensions"
High Dimensional Hamilton-Jacobi PDEs 2020 Workshop I: High Dimensional Hamilton-Jacobi Methods in Control and Differential Games "Al'brekht’s Method in Infinite Dimensions" Arthur Krener, Naval Postgraduate School Abstract: Al'brekht's method is a way optimally stabilize a finite dimens
From playlist High Dimensional Hamilton-Jacobi PDEs 2020
Entropy Growth during Free Expansion of an Ideal Fermi Gas by Saurav Pandey
ICTS In-house 2022 Organizers: Chandramouli, Omkar, Priyadarshi, Tuneer Date and Time: 20th to 22nd April, 2022 Venue: Ramanujan Hall inhouse@icts.res.in An exclusive three-day event to exchange ideas and research topics amongst members of ICTS.
From playlist ICTS In-house 2022
David Roberts, Hurwitz Belyi maps
VaNTAGe seminar, October 12, 2021 License: CC-BY-NC-SA
From playlist Belyi maps and Hurwitz spaces
