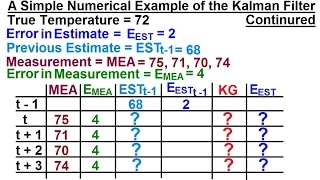
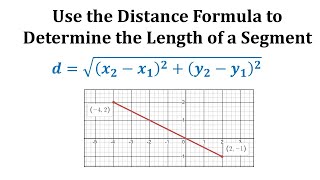
Point estimation
In statistics, point estimation involves the use of sample data to calculate a single value (known as a point estimate since it identifies a point in some parameter space) which is to serve as a "best guess" or "best estimate" of an unknown population parameter (for example, the population mean). More formally, it is the application of a point estimator to the data to obtain a point estimate. Point estimation can be contrasted with interval estimation: such interval estimates are typically either confidence intervals, in the case of frequentist inference, or credible intervals, in the case of Bayesian inference. More generally, a point estimator can be contrasted with a set estimator. Examples are given by confidence sets or credible sets. A point estimator can also be contrasted with a distribution estimator. Examples are given by confidence distributions, randomized estimators, and Bayesian posteriors. (Wikipedia).