Graphical models | Markov networks
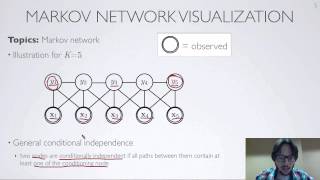
Markov random field
In the domain of physics and probability, a Markov random field (MRF), Markov network or undirected graphical model is a set of random variables having a Markov property described by an undirected graph. In other words, a random field is said to be a Markov random field if it satisfies Markov properties. The concept originates from the Sherrington–Kirkpatrick model. A Markov network or MRF is similar to a Bayesian network in its representation of dependencies; the differences being that Bayesian networks are directed and acyclic, whereas Markov networks are undirected and may be cyclic. Thus, a Markov network can represent certain dependencies that a Bayesian network cannot (such as cyclic dependencies); on the other hand, it can't represent certain dependencies that a Bayesian network can (such as induced dependencies). The underlying graph of a Markov random field may be finite or infinite. When the joint probability density of the random variables is strictly positive, it is also referred to as a Gibbs random field, because, according to the Hammersley–Clifford theorem, it can then be represented by a Gibbs measure for an appropriate (locally defined) energy function. The prototypical Markov random field is the Ising model; indeed, the Markov random field was introduced as the general setting for the Ising model. In the domain of artificial intelligence, a Markov random field is used to model various low- to mid-level tasks in image processing and computer vision. (Wikipedia).