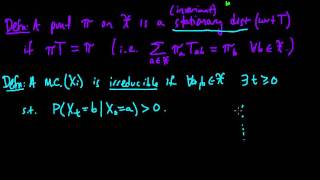Markov models | Markov processes
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It is named after the Russian mathematician Andrey Markov. The term strong Markov property is similar to the Markov property, except that the meaning of "present" is defined in terms of a random variable known as a stopping time. The term Markov assumption is used to describe a model where the Markov assumption is assumed to hold, such as a hidden Markov model. A Markov random field extends this property to two or more dimensions or to random variables defined for an interconnected network of items. An example of a model for such a field is the Ising model. A discrete-time stochastic process satisfying the Markov property is known as a Markov chain. (Wikipedia).