
👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

What is an equilateral triangle
👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

What is an equiangular triangle
👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

On minimizers and critical points for anisotropic isoperimetric problems - Robin Neumayer
Variational Methods in Geometry Seminar Topic: On minimizers and critical points for anisotropic isoperimetric problems Speaker: Robin Neumayer Affiliation: Member, School of Mathematics Date: February 19, 2019 For more video please visit http://video.ias.edu
From playlist Variational Methods in Geometry

👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

V. Franceschi - Sub-riemannian soap bubbles
The aim of this seminar is to present some results about minimal bubble clusters in some sub-Riemannian spaces. This amounts to finding the best configuration of m ∈ N regions in a manifold enclosing given volumes, in order to minimize their total perimeter. In a n-dimensional sub-Riemanni
From playlist Journées Sous-Riemanniennes 2018

Ilaria Fragalà: Some new inequalities for the Cheeger constant
Abstract: We discuss some new results for the Cheeger constant in dimension two, including: - a polygonal version of Faber-Krahn inequality; - a reverse isoperimetric inequality for convex bodies; - a Mahler-type inequality in the axisymmetric setting; - asymptotic behaviour of optimal par
From playlist Control Theory and Optimization

Colloquium MathAlp 2016 - Michel Ledoux
Isopérimétrie dans les espaces métriques mesurés Le problème isopérimétrique (à volume donné, minimiser la mesure de bord, et déterminer les ensembles extrémaux), remonte aux temps les plus anciens. Tout à la fois, il peut se formuler de façon générale dans un espace métrique mesuré, et d
From playlist Colloquiums MathAlp

Joe Neeman: Gaussian isoperimetry and related topics I
The Gaussian isoperimetric inequality gives a sharp lower bound on the Gaussian surface area of any set in terms of its Gaussian measure. Its dimension-independent nature makes it a powerful tool for proving concentration inequalities in high dimensions. We will explore several consequence
From playlist Winter School on the Interplay between High-Dimensional Geometry and Probability
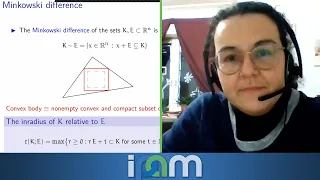
Eugenia Saorin-Gomez - Inner parallel bodies & the Isoperimetric Quotient
Recorded 10 February 2022. Eugenia Saorin-Gomez of the Universität Bremen presents "Inner parallel bodies & the Isoperimetric Quotient" at IPAM's Calculus of Variations in Probability and Geometry Workshop. Abstract: The so-called Minkowski difference of convex bodies (compact and convex s
From playlist Workshop: Calculus of Variations in Probability and Geometry

👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

Joe Neeman: Gaussian isoperimetry and related topics II
The Gaussian isoperimetric inequality gives a sharp lower bound on the Gaussian surface area of any set in terms of its Gaussian measure. Its dimension-independent nature makes it a powerful tool for proving concentration inequalities in high dimensions. We will explore several consequence
From playlist Winter School on the Interplay between High-Dimensional Geometry and Probability

Joe Neeman: Gaussian isoperimetry and related topics III
The Gaussian isoperimetric inequality gives a sharp lower bound on the Gaussian surface area of any set in terms of its Gaussian measure. Its dimension-independent nature makes it a powerful tool for proving concentration inequalities in high dimensions. We will explore several consequence
From playlist Winter School on the Interplay between High-Dimensional Geometry and Probability
From playlist Dimensions Arabe/Arabic / العربية
From playlist Dimensions Arabe/Arabic / العربية

Yevgeny Liokumovich (9/10/21): Urysohn width, isoperimetric inequalities and scalar curvature
There exists a positive constant c(n) with the following property. If M is a metric space, such that every ball B of radius 1 in M has Hausdorff n-dimensional measure less than c(n), then there exists a continuous map f from M to (n-1)-dimensional simplicial complex, such that every pre-im
From playlist Vietoris-Rips Seminar

Santosh Vempala - Gibbs Sampling for Convex Bodies and an L_0 Isoperimetric Inequality
Recorded 10 February 2022. Santosh Vempala of Georgia Institute of Technology, Computer Science, presents "Gibbs Sampling for Convex Bodies and an L_0 Isoperimetric Inequality" at IPAM's Calculus of Variations in Probability and Geometry Workshop. Abstract: Gibbs sampling, also known as C
From playlist Workshop: Calculus of Variations in Probability and Geometry

👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties