
Senior Chemistry lesson on reaction kinetics and what the equilibrium constant represents and how to calculate.
From playlist Chemistry

Physics - Thermodynamics 2: Ch 32.1 Def. and Terms (9 of 23) What is the Gas Constant?
Visit http://ilectureonline.com for more math and science lectures! In this video I will give and explain what is the gas constant and how it was determined. Next video in this series can be seen at: https://youtu.be/8N8TN0L5xiQ
From playlist PHYSICS 32.1 THERMODYNAMICS 2 BASIC TERMS

How an Equilibrium Constant varies with Temperature - Thermodynamics - Physical Chemistry
Deriving a quantitative relationship to show how an equilibrium constant varies with temperature and so showing were Le Chatelier's Principle comes from in this context. Along the way, the Gibbs-Helmholtz van't Hoff equations are derived and used. My video for deriving the thermodynamics
From playlist Introductory Thermodynamics

From playlist Courses and Series
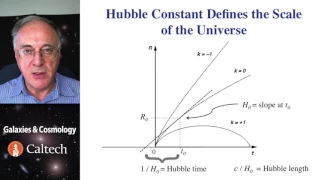
From playlist Courses and Series

The Professor discusses why "papers" are so important to scientists.
From playlist Chem Definition - Periodic Videos

Nicolás García Trillos: "From clustering with graph cuts to isoperimetric inequalities..."
High Dimensional Hamilton-Jacobi PDEs 2020 Workshop II: PDE and Inverse Problem Methods in Machine Learning "From clustering with graph cuts to isoperimetric inequalities: quantitative convergence rates of Cheeger cuts on data clouds" Nicolás García Trillos - University of Wisconsin-Madis
From playlist High Dimensional Hamilton-Jacobi PDEs 2020

Ilaria Fragalà: Some new inequalities for the Cheeger constant
Abstract: We discuss some new results for the Cheeger constant in dimension two, including: - a polygonal version of Faber-Krahn inequality; - a reverse isoperimetric inequality for convex bodies; - a Mahler-type inequality in the axisymmetric setting; - asymptotic behaviour of optimal par
From playlist Control Theory and Optimization

Higher-Order Cheeger Inequalities - Luca Trevisan
Luca Trevisan Stanford University March 27, 2012 A basic fact of algebraic graph theory is that the number of connected components in an undirected graph is equal to the multiplicity of the eigenvalue zero in the Laplacian matrix of the graph. In particular, the graph is disconnected if an
From playlist Mathematics

Paolo Piazza: The Novikov conjecture on stratified spaces
A Cheeger space is a smoothly stratified pseudomanifold which is in general non-Witt but that admits an additional structure along the strata that allows for the definition of ideal boundary conditions. An interesting example is given by the reductive Borel-Serre compactification of a Hilb
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

037 - The Rate Constant In this video Paul Andersen describes the characteristics of the rate constant in chemical reactions. The rate constant is highly variable in reactions and must be determined experimentally. The rate constant is dependent on both temperature and the presence of a
From playlist AP Chemistry Video Essentials

The structure of noncollapsed Gromov-Hausdorff limit spaces - Jeff Cheeger [2017]
slides for this talk: https://drive.google.com/file/d/1pvkn4Qew5ZHrDpvs9txzFOsFFDqYfA3E/view?usp=sharing Name: Jeff Cheeger Event: Workshop: Geometry of Manifolds Event URL: view webpage Title: The structure of noncollapsed Gromov-Hausdorff limit spaces with Ricci Curvature bounded below
From playlist Mathematics

Yuansi Chen: Recent progress on the KLS conjecture
Kannan, Lovász and Simonovits (KLS) conjectured in 1995 that the Cheeger isoperimetric coefficient of any log-concave density is achieved by half-spaces up to a universal constant factor. This conjecture also implies other important conjectures such as Bourgain’s slicing conjecture (1986)
From playlist Workshop: High dimensional measures: geometric and probabilistic aspects

D. Semola - Boundary regularity and stability under lower Ricci bounds
The theory of non smooth spaces with lower Ricci Curvature bounds has undergone huge developments in the last thirty years. On the one hand the impetus came from Gromov’s precompactness theorem and the Cheeger-Colding theory of Ricci limit spaces. On the other hand “synthetic” theories of
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

D. Semola - Boundary regularity and stability under lower Ricci bounds (version temporaire)
The theory of non smooth spaces with lower Ricci Curvature bounds has undergone huge developments in the last thirty years. On the one hand the impetus came from Gromov’s precompactness theorem and the Cheeger-Colding theory of Ricci limit spaces. On the other hand “synthetic” theories of
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

T. Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 2)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem for manifolds with a lower bound on the Ricci curvature, and derive some important consequences
From playlist Ecole d'été 2016 - Analyse géométrique, géométrie des espaces métriques et topologie

JEE Main Physics Thermodynamics #2 Thermodynamic Process
Visit http://ilectureonline.com for more math and science lectures! To donate: http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 Match List I with List II: List I List II a) isothermal (i) pressure constant b) isochoric
From playlist JEE (MAIN) PHYSICS THERMODYNAMICS

T. Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 3)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem for manifolds with a lower bound on the Ricci curvature, and derive some important consequences
From playlist Ecole d'été 2016 - Analyse géométrique, géométrie des espaces métriques et topologie

