
Definitions, specification and interpretation | Arithmetic and Geometry Math Foundations 44
We discuss important meta-issues regarding definitions and specification in mathematics. We also introduce the idea that mathematical definitions, expressions, formulas or theorems may support a variety of possible interpretations. Examples use our previous definitions from elementary ge
From playlist Math Foundations

What is a number? | Arithmetic and Geometry Math Foundations 1 | N J Wildberger
The first of a series that will discuss foundations of mathematics. Contains a general introduction to the series, and then the beginnings of arithmetic with natural numbers. This series will methodically develop a lot of basic mathematics, starting with arithmetic, then geometry, then alg
From playlist Math Foundations

The essential dichotomy underlying mathematics | Data Structures Math Foundations 186
What lies at the very core of mathematics? What is mathematics ultimately about, once we strip away all the hoopla and complexity? In this video I give you my answer to this intriguing question. Surprisingly, it is not really the natural numbers: they are fundamental, but not the most fund
From playlist Math Foundations

What is the Fundamental theorem of Algebra, really? | Abstract Algebra Math Foundations 217
Here we give restatements of the Fundamental theorems of Algebra (I) and (II) that we critiqued in our last video, so that they are now at least meaningful and correct statements, at least to the best of our knowledge. The key is to abstain from any prior assumptions about our understandin
From playlist Math Foundations

The basic framework for geometry (II) | Arithmetic and Geometry Math Foundations 24 | N J Wildberger
We discuss parallel and perpendicular lines, and basic notions relating to triangles, including the notion of a side and a vertex of a triangle. This lecture is part of the MathFoundations series, which tries to lay out proper foundations for mathematics, and will not shy away from discus
From playlist Math Foundations

Laws of Arithmetic | Arithmetic and Geometry Math Foundations 3 | N J Wildberger
We explain why the basic laws for addition and multiplication hold, using a model of natural numbers as strings of ones. These are the basic operations, and all students should have some understanding that these operations actually satisfy laws, that are then tools we can use to make calcu
From playlist Math Foundations

The problem with `functions' | Arithmetic and Geometry Math Foundations 42a
[First of two parts] Here we address a core logical problem with modern mathematics--the usual definition of a `function' does not contain precise enough bounds on the nature of the rules or procedures (or computer programs) allowed. Here we discuss the difficulty in the context of funct
From playlist Math Foundations
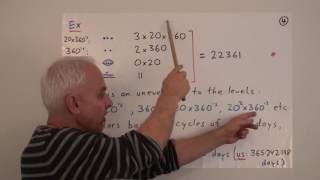
The curious role of "nothing" in mathematics | Data Structures Math Foundations 187
The role of "nothing" in mathematics is a curious one. In this video we discuss how different cultures interpreted the nebulous concept, particularly how the number zero was eventually introduced by the Hindus. We also discuss how modern physics has changed its view to empty space in the l
From playlist Math Foundations

The realm of natural numbers | Data structures in Mathematics Math Foundations 155
Here we look at a somewhat unfamiliar aspect of arithmetic with natural numbers, motivated by operations with multisets, and ultimately forming a main ingredient for that theory. We look at natural numbers, together with 0, under three operations: addition, union and intersection. We will
From playlist Math Foundations

Benedikt Ahrens - Univalent Foundations and the UniMath library - IPAM at UCLA
Recorded 13 February 2023. Benedikt Ahrens of Delft University of Technology presents "Univalent Foundations and the UniMath library" at IPAM's Machine Assisted Proofs Workshop. Abstract: Univalent Foundations (UF) were designed by Voevodsky as a foundation of mathematics that is "invarian
From playlist 2023 Machine Assisted Proofs Workshop

IMS Public Lecture: Foundations of Mathematics: An Optimistic Message
Stephen G. Simpson, Pennsylvania State University, USA
From playlist Public Lectures

Foundation: Are We Predictable?
In which Jeff Goldblum, lemmings, and a pixelated photo of Obama help me uncover the mathematical reality of Isaac Asimov’s psychohistory. In his Foundation book series, Asimov invented psychohistory, a scientific description of history that can predict the future. This video asks whether
From playlist Video Essays

Séminaire Bourbaki - 21/06/2014 - 3/4 - Thomas C. HALES
Developments in formal proofs A for mal proof is a proof that can be read and verified by computer, directly from the fundamental rules of logic and the foundational axioms of mathematics. The technology behind for mal proofs has been under development for decades and grew out of efforts i
From playlist Bourbaki - 21 juin 2014

What if Current Foundations of Mathematics are Inconsistent? | Vladimir Voevodsky
Vladimir Voevodsky, Professor, School of Mathematics, Institute for Advanced Study http://www.ias.edu/people/faculty-and-emeriti/voevodsky In this lecture, Professor Vladimir Voevodsky begins with Gödel's second incompleteness theorem to discuss the possibility that the formal theory of f
From playlist Mathematics

Story telling (in mathematics and music) - Will Troiani
Will explores the relationship between music and mathematics. He suggests that narratives behind the foundations are part of the foundations themselves, and use the example of topology to demonstrate this. Chess is also used to illustrate how learning the basic rules and concepts can lead
From playlist Anything At All seminar
5 - Kick-off afternoon : Vladimir Voevodsky, Univalent Foundations
Vladimir Voevodsky (Institute for Advanced Study, Princeton): Univalent Foundations - new type-theoretic foundations of mathematics
From playlist T2-2014 : Semantics of proofs and certified mathematics

Strengthening Mathematics in the Developing World – ICM2018
IMU Discussion Panels Panel 4 - Strengthening Mathematics in the Developing World Moderator: Angel Pineda Panelists: Wandera Ogana, Marie-Françoise Roy, Yuri Tschinkel, Paolo Piccione, Jose Maria Balmaceda, Nouzha El Yacoubi, Alejandro Jofré © ICM 2018 – International Congress of Math
From playlist IMU Discussion Panels

The Foundations seminar returns for Season 2 on 21/7/22. This time Will Troiani and Billy Snikkers will present the Ax-Grothendieck theorem, via model theory, an interesting crossover between logic and geometry. To join in head over to https://www.metauni.org and join the metauni Discord
From playlist Foundations seminar

MF150: What exactly is a set? | Data Structures in Mathematics Math Foundations | NJ Wildberger
What exactly is a set?? This is a crucial question in the modern foundations of mathematics. Here we begin an examination of this thorny issue, first by discussing the usual English usage of the term, as well as alternate terms, such as collection, aggregate, bunch, class, menagerie etc th
From playlist Math Foundations
