Introduction to Set Theory (Discrete Mathematics)
Introduction to Set Theory (Discrete Mathematics) This is a basic introduction to set theory starting from the very beginning. This is typically found near the beginning of a discrete mathematics course in college or at the beginning of other advanced mathematics courses. ***************
From playlist Set Theory

We give some basic definitions and notions associated with sets. In particular, we describe sets via the "roster method", via a verbal description, and with set-builder notation. We also give an example of proving the equality of two sets. Please Subscribe: https://www.youtube.com/michael
From playlist Proof Writing

Set Theory (Part 2): ZFC Axioms
Please feel free to leave comments/questions on the video and practice problems below! In this video, I introduce some common axioms in set theory using the Zermelo-Fraenkel w/ choice (ZFC) system. Five out of nine ZFC axioms are covered and the remaining four will be introduced in their
From playlist Set Theory by Mathoma
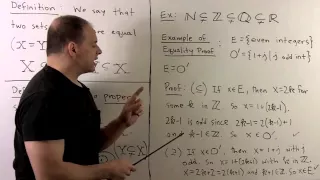
Basic Methods: We introduce basic notions from naive set theory, including sets, elements, and subsets. We give examples of showing two sets are equal by mutual inclusion. Then we define the power set and note Russell's paradox.
From playlist Math Major Basics

Introduction to Sets and Set Notation
This video defines a set, special sets, and set notation.
From playlist Sets (Discrete Math)

Introduction to sets || Set theory Overview - Part 2
A set is the mathematical model for a collection of different things; a set contains elements or members, which can be mathematical objects of any kind: numbers, symbols, points in space, lines, other geometrical shapes, variables, or even other #sets. The #set with no element is the empty
From playlist Set Theory

Set Theory (Part 1): Notation and Operations
Please feel free to leave comments/questions on the video and practice problems below! In this video series, we'll explore the basics of set theory. I assume no experience with set theory in the video series and anyone who's "been around town" in math should understand the videos. To make
From playlist Set Theory by Mathoma

Set Theory (Part 3): Ordered Pairs and Cartesian Products
Please feel free to leave comments/questions on the video and practice problems below! In this video, I cover the Kuratowski definition of ordered pairs in terms of sets. This will allow us to speak of relations and functions in terms of sets as the basic mathematical objects and will ser
From playlist Set Theory by Mathoma

Introduction to sets || Set theory Overview - Part 1
A set is the mathematical model for a collection of different things; a set contains elements or members, which can be mathematical objects of any kind: numbers, symbols, points in space, lines, other geometrical shapes, variables, or even other #sets. The #set with no element is the empty
From playlist Set Theory

Séminaire Bourbaki - 21/06/2014 - 3/4 - Thomas C. HALES
Developments in formal proofs A for mal proof is a proof that can be read and verified by computer, directly from the fundamental rules of logic and the foundational axioms of mathematics. The technology behind for mal proofs has been under development for decades and grew out of efforts i
From playlist Bourbaki - 21 juin 2014

Why Algebraic Data Types Are Important
Strong static typing detects a lot of bugs at compile time, so why would anyone prefer to program in JavaScript or Python? The main reason is that type systems can be extremely complex, often with byzantine typing rules (C++ comes to mind). This makes generic programming a truly dark art.
From playlist Functional Programming

Fabian Immler, Carnegie Mellon University Formal mathematics and a proof of chaos Formal proof has been successfully applied to the verification of hardware and software systems. But formal proof is also applicable to mathematics: proofs can be checked with ultimate rigor and one can bui
From playlist Fall 2019 Kolchin Seminar in Differential Algebra

Univalent Foundations Seminar - Steve Awodey
Steve Awodey Carnegie Mellon University; Member, School of Mathematics November 19, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

Category Theory 1.1: Motivation and Philosophy
Motivation and philosophy
From playlist Category Theory

Furio Honsell - Tribute to Ennio De Giorgi - 20 September 2016
Honsell, Furio "Implementing Cantor’s paradise in constructive type theory"
From playlist A Mathematical Tribute to Ennio De Giorgi

Inference: A Logical-Philosophical Perspective - Moderated Conversation w/ A.C. Paseau and Gila Sher
Inference: A Logical-Philosophical Perspective. Moderated Conversation with Gila Sher, Department of Philosophy, University of California, San Diego on the talk by Alexander Paseau, Faculty of Philosophy, University of Oxford. The Franke Program in Science and the Humanities Understandi
From playlist Franke Program in Science and the Humanities

Machine-Assisted Proofs – ICM2018
IMU Discussion Panels Panel 2 - Machine-Assisted Proofs Moderator: James Davenport Panelists: Luís Cruz-Filipe, Harald Helfgott, James Maynard, Bjorn Poonen, Pham Huu Tiep © ICM 2018 – International Congress of Mathematicians www.icm2018.org Os direitos sobre todo o material des
From playlist IMU Discussion Panels

This video introduces the basic vocabulary used in set theory. http://mathispower4u.wordpress.com/
From playlist Sets

After Math: Reasoning, Proving, and Computing in the Postwar United States - Stephanie Dick
More videos on http://video.ias.edu
From playlist Historical Studies