
Time Reversal Symmetry Operator | Quantum Mechanics
In this video, we will discuss the time reversal operator in quantum mechanics. According to Wigner's theorem, physical symmetries in a Hilbert space can be represented mathematically either by unitary operators or by anti-unitary operators. The time reversal operator is a common example o
From playlist Quantum Mechanics, Quantum Field Theory

Ch 11: What are unitary operators? | Maths of Quantum Mechanics
Hello! This is the eleventh chapter in my series "Maths of Quantum Mechanics." In this episode, we'll define unitary operators and understand how they preserve the inner product. We'll then show how unitary transformations preserve probability in quantum mechanics, and why that makes it a
From playlist Maths of Quantum Mechanics

Ever heard of Quantum Operators and Commutators? (Explained for Beginners)!
What is a quantum operator? And just how useful are quantum commutators? Find out how they help us understand the Ehrenfest Theorem! Hi everyone, I'm back with a new video! This time it's the first in a two-part mini-series on one of the coolest theorems in quantum mechanics - Ehrenfest's
From playlist Quantum Physics by Parth G

Basis and Quantum State; Quantum Operators
In this video, we review concepts of quantum basis and quantum state (in a finite-dimensional Hilbert space) and how to implement them in the Wolfram Quantum Framework. We also discuss the basis transformation. For more info and examples, please visit the Wolfram Quantum Framework resource
From playlist Daily Study Group: Quantum Computation Framework
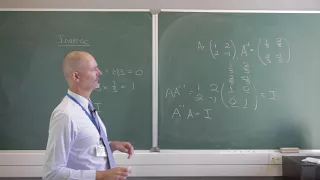
The inverse of a matrix is a similarly sized matrix such that the multiplication of the two matrices results in the identity matrix. In this video we look at an example of this. You can learn more about Mathematica on my Udemy course at https://www.udemy.com/mathematica/ PS! Wait until
From playlist Introducing linear algebra

Properties of the Time Reversal Operator | Quantum Mechanics
In this video, we will discuss some properties of the time reversal operator in quantum mechanics. We will first talk about physical properties, for instance how certain observables are affected by a time reversal, and then also discuss mathematical properties of anti-unitary operators.
From playlist Quantum Mechanics, Quantum Field Theory

Hermitian Operators (Self-Adjoint Operators) | Quantum Mechanics
In this video, we will talk about Hermitian operators in quantum mechanics. If an operator A is a Hermitian operator, then it is the same as its adjoint operator A-dagger, which is defined via this equation here. Usually, the terms "Hermitian" and "self adjoint" are used interchangeably, h
From playlist Quantum Mechanics, Quantum Field Theory

This video discusses unitary matrix transformations and how they relate to the geometry of the singular value decomposition (SVD). These lectures follow Chapter 1 from: "Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control" by Brunton and Kutz Amazon: h
From playlist Data-Driven Science and Engineering

Representation Theory: We explain unitarity and invariant inner products for representations of finite groups. Full reducibility of such representations is derived. Course materials, including problem sets and solutions, available at http://mathdoctorbob.org/UR-RepTheory.html
From playlist Representation Theory

Lara Ismert: "Heisenberg Pairs on Hilbert C*-modules"
Actions of Tensor Categories on C*-algebras 2021 "Heisenberg Pairs on Hilbert C*-modules" Lara Ismert - Embry-Riddle Aeronautical University, Mathematics Abstract: Roughly speaking, a Heisenberg pair on a Hilbert space is a pair of self-adjoint operators (A,B) which satisfy the Heisenber
From playlist Actions of Tensor Categories on C*-algebras 2021

36 entangled officers of Euler: A quantum solution to a classically... by Arul Lakshminarayan
Colloquium: 36 entangled officers of Euler: A quantum solution to a classically impossible problem Speaker: Arul Lakshminarayan (IIT Madras, Chennai) Date: Mon, 06 June 2022, 15:30 to 17:00 Venue: Online and Madhava Lecture Hall Abstract The 36 officers problem of Euler is a well-known i
From playlist ICTS Colloquia

Two variations on operator spreading by Shivaji Sondhi
ORGANIZERS : Pallab Basu, Avinash Dhar, Rajesh Gopakumar, R. Loganayagam, Gautam Mandal, Shiraz Minwalla, Suvrat Raju, Sandip Trivedi and Spenta Wadia DATE : 21 May 2018 to 02 June 2018 VENUE : Ramanujan Lecture Hall, ICTS Bangalore In the past twenty years, the discovery of the AdS/C
From playlist AdS/CFT at 20 and Beyond

Stanford Seminar - Highly optimized quantum circuits synthesized via data-flow engines
Peter Rakyta, Department of Physics of Complex Systems at Eötvös Loránd University November 9, 2022 The formulation of quantum programs in terms of the fewest number of gate operations is crucial to retrieve meaningful results from the noisy quantum processors accessible these days. In th
From playlist Stanford EE380-Colloquium on Computer Systems - Seminar Series

Tomaž Prosen: "Exactly solved models of chaotic many-body dynamics"
Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021 Workshop II: Tensor Network States and Applications "Exactly solved models of chaotic many-body dynamics" Tomaž Prosen - University of Ljubljana Abstract: One should be amazed with an unreasonable effectivene
From playlist Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021

Non-equilibrium dynamics in dual-unitary quantum circuits by Bruno Bertini
PROGRAM THERMALIZATION, MANY BODY LOCALIZATION AND HYDRODYNAMICS ORGANIZERS: Dmitry Abanin, Abhishek Dhar, François Huveneers, Takahiro Sagawa, Keiji Saito, Herbert Spohn and Hal Tasaki DATE : 11 November 2019 to 29 November 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore How do is
From playlist Thermalization, Many Body Localization And Hydrodynamics 2019

Recovering quantum gates from few average fidelities - R. Kueng - Workshop 1 - CEB T2 2018
Richard Kueng (California Institute of Technology) / 17.05.2018 Recovering quantum gates from few average fidelities Characterizing quantum processes is a key task for the development of quantum technologies, especially at the noisy intermediate scale of today’s devices. One method for
From playlist 2018 - T2 - Measurement and Control of Quantum Systems: Theory and Experiments

Winter Theory School 2022: Adam Nahum
Random circuits as models for chaotic dynamics
From playlist Winter Theory 2022

In this section I introduce plane autonomous systems, which form beautiful and useful vector fields.
From playlist A Second Course in Differential Equations