
Math 139 Fourier Analysis Lecture 38: Finishing proof of Dirichlet's theorem
Showing the non-vanishing of the L-function for real Dirichlet characters. Approximation of L(1,X) with hyperbolic sums to finish the theorem.
From playlist Course 8: Fourier Analysis

Math 139 Fourier Analysis Lecture 35: Dirichlet's theorem pt. 2
Dirichlet's theorem: reduction of the problem. Dirichlet L-function. Product formula for L-functions. Extension of the logarithm to complex numbers. Convergence of infinite products.
From playlist Course 8: Fourier Analysis

Introduction to number theory lecture 51. Proof of Dirichlet's theorem
This lecture is part of my Berkeley math 115 course "Introduction to number theory" For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj53L8sMbzIhhXSAOpuZ1Fov8 We show how to prove Dirichlet's theorem on primes in arithmetic progressions, assuming tha
From playlist Introduction to number theory (Berkeley Math 115)

Representation theory: Dirichlet's theorem
In this talk we see how to use characters of finite abelian groups to prove Dirichlet's theorem that there are infinitely many primes in certain arithmetic progressions. We first recall Euler's proof that there are infinitely many primes, which is the simplest case of Dirichlet's proof. T
From playlist Representation theory

Theory of numbers: Dirichlet series
This lecture is part of an online undergraduate course on the theory of numbers. We describe the correspondence between Dirichlet series and arithmetic functions, and work out the Dirichlet series of the arithmetic functions in the previous lecture. Correction: Dave Neary pointed out t
From playlist Theory of numbers

Math 139 Fourier Analysis Lecture 37: Dirichlet's theorem pt.4
Defining the logarithm of an L-function. Second reduction of the problem: proving non-vanishing of the L-function. Case of complex Dirichlet characters.
From playlist Course 8: Fourier Analysis

Math 139 Fourier Analysis Lecture 36: Dirichlet's theorem pt. 3
Proof of the product formula for Dirichlet L-functions. Defining the logarithm of an L-function: technical proposition. Key lemma.
From playlist Course 8: Fourier Analysis

Linear Equations in Primes and Nilpotent Groups - Tamar Ziegler
Tamar Ziegler Technion--Israel Institute of Technology January 30, 2011 A classical theorem of Dirichlet establishes the existence of infinitely many primes in arithmetic progressions, so long as there are no local obstructions. In 2006 Green and Tao set up a program for proving a vast gen
From playlist Mathematics

(ML 7.7.A1) Dirichlet distribution
Definition of the Dirichlet distribution, what it looks like, intuition for what the parameters control, and some statistics: mean, mode, and variance.
From playlist Machine Learning
Half-Isolated Zeros and Zero-Density Estimates - Kyle Pratt
50 Years of Number Theory and Random Matrix Theory Conference Topic: Half-Isolated Zeros and Zero-Density Estimates Speaker: Kyle Pratt Affiliation: University of Oxford Date: June 23, 2022 We introduce a new zero-detecting method which is sensitive to the vertical distribution of zeros
From playlist Mathematics

James Maynard: Half-isolated zeros and zero-density estimates
We introduce a new zero-detecting method which is sensitive to the vertical distribution of zeros of the zeta function. This allows us to show that there are few 'half-isolated' zeros, and allows us to improve the classical zero density result to N(σ,T)≪T24(1−σ)/11+o(1) if we assume that t
From playlist Seminar Series "Harmonic Analysis from the Edge"

Bourbaki - 18/06/2016 - 4/4 - Kannan SOUNDARARAJAN
Kannan SOUNDARARAJAN — The Liouville function in short intervals [after Matomäki and Radziwiłł] The Liouville function λ(n) is a completely multiplicative function, taking the value 1 if n has an even number of prime factors (counted with multiplicity) and −1 if n has an odd number of prim
From playlist Bourbaki - 18 juin 2016

Theory of numbers:Introduction
This lecture is part of an online undergraduate course on the theory of numbers. This is the introductory lecture, which gives an informal survey of some of the topics to be covered in the course, such as Diophantine equations, quadratic reciprocity, and binary quadratic forms.
From playlist Theory of numbers

Introduction to number theory lecture 52. Nonvanishing of L series at s=1.
This lecture is part of my Berkeley math 115 course "Introduction to number theory" For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj53L8sMbzIhhXSAOpuZ1Fov8 We sketch how to show that Dirichlet L functions do not vanish at s=1, completing the proo
From playlist Introduction to number theory (Berkeley Math 115)

The Abel Prize announcement 2020 — Hillel Furstenberg & Gregory Margulis
0:50 The Abel Prize announced by Hans Petter Graver, President of The Norwegian Academy of Science and Letters 1:37 Citation by Hans Munthe-Kaas, Chair of the Abel committee 9:28 Popular presentation of the prize winners work by Alex Bellos, British writer, and science communicator 16:21 I
From playlist Gregory Margulis

Introduction to number theory lecture 2: Survey.
This lecture is part of my Berkeley math 115 course "Introduction to number theory" We continue the survey of some problems in number theory, and discuss congruences, quadratic reciprocity, additive number theory, recreational number theory, and partitions. For the other lectures in the
From playlist Introduction to number theory (Berkeley Math 115)
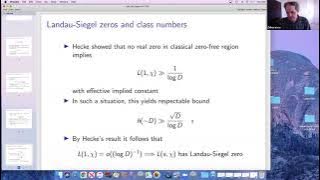
Some remarks on Landau--Siegel zeros - Alexandru Zaharescu
Joint IAS/Princeton University Number Theory Seminar Some remarks on Landau--Siegel zeros Alexandru Zaharescu University of Illinois at Urbana–Champaign Date: March 11, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

Theory of numbers: Gauss's lemma
This lecture is part of an online undergraduate course on the theory of numbers. We describe Gauss's lemma which gives a useful criterion for whether a number n is a quadratic residue of a prime p. We work it out explicitly for n = -1, 2 and 3, and as an application prove some cases of Di
From playlist Theory of numbers
