Cubic plane curve
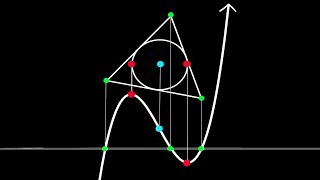
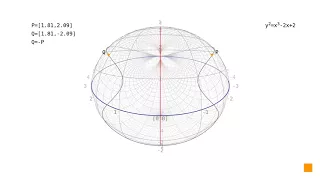
In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equation applied to homogeneous coordinates for the projective plane; or the inhomogeneous version for the affine space determined by setting z = 1 in such an equation. Here F is a non-zero linear combination of the third-degree monomials These are ten in number; therefore the cubic curves form a projective space of dimension 9, over any given field K. Each point P imposes a single linear condition on F, if we ask that C pass through P. Therefore, we can find some cubic curve through any nine given points, which may be degenerate, and may not be unique, but will be unique and non-degenerate if the points are in general position; compare to two points determining a line and how five points determine a conic. If two cubics pass through a given set of nine points, then in fact a pencil of cubics does, and the points satisfy additional properties; see Cayley–Bacharach theorem. A cubic curve may have a singular point, in which case it has a parametrization in terms of a projective line. Otherwise a non-singular cubic curve is known to have nine points of inflection, over an algebraically closed field such as the complex numbers. This can be shown by taking the homogeneous version of the Hessian matrix, which defines again a cubic, and intersecting it with C; the intersections are then counted by Bézout's theorem. However, only three of these points may be real, so that the others cannot be seen in the real projective plane by drawing the curve. The nine inflection points of a non-singular cubic have the property that every line passing through two of them contains exactly three inflection points. The real points of cubic curves were studied by Isaac Newton. The real points of a non-singular projective cubic fall into one or two 'ovals'. One of these ovals crosses every real projective line, and thus is never bounded when the cubic is drawn in the Euclidean plane; it appears as one or three infinite branches, containing the three real inflection points. The other oval, if it exists, does not contain any real inflection point and appears either as an oval or as two infinite branches. Like for conic sections, a line cuts this oval at, at most, two points. A non-singular plane cubic defines an elliptic curve, over any field K for which it has a point defined. Elliptic curves are now normally studied in some variant of Weierstrass's elliptic functions, defining a quadratic extension of the field of rational functions made by extracting the square root of a cubic. This does depend on having a K-rational point, which serves as the point at infinity in Weierstrass form. There are many cubic curves that have no such point, for example when K is the rational number field. The singular points of an irreducible plane cubic curve are quite limited: one double point, or one cusp. A reducible plane cubic curve is either a conic and a line or three lines, and accordingly have two double points or a tacnode (if a conic and a line), or up to three double points or a single triple point (concurrent lines) if three lines. (Wikipedia).