
The Angles Created from Lines and a Transversal
👉 Learn how to identify angles from a figure. This video explains how to solve problems using angle relationships between parallel lines and transversal. We'll determine the solution given, corresponding, alternate interior and exterior. All the angle formed by a transversal with two paral
From playlist Parallel Lines and a Transversal
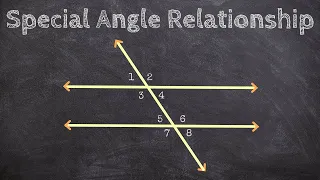
Lines and a Transversal - How To Label Special Angle Relationships
👉 Learn how to identify angles from a figure. This video explains how to solve problems using angle relationships between parallel lines and transversal. We'll determine the solution given, corresponding, alternate interior and exterior. All the angle formed by a transversal with two paral
From playlist Parallel Lines and a Transversal
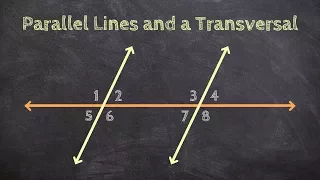
Classifying Angles Given Parallel Lines and a Transversal
👉 Learn how to identify angles from a figure. This video explains how to solve problems using angle relationships between parallel lines and transversal. We'll determine the solution given, corresponding, alternate interior and exterior. All the angle formed by a transversal with two paral
From playlist Parallel Lines and a Transversal
Learn to Find Corresponding Angles From a Figure
👉 Learn how to identify angles from a figure. This video explains how to solve problems using angle relationships between parallel lines and transversal. We'll determine the solution given, corresponding, alternate interior and exterior. All the angle formed by a transversal with two paral
From playlist Parallel Lines and a Transversal
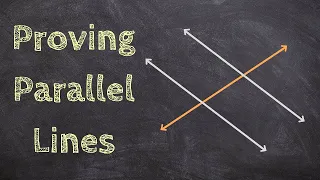
Proving Parallel Lines with Angle Relationships
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal
What are the Angle Relationships for Parallel Lines and a Transversal
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal

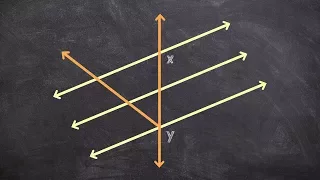
What are parallel lines and a transversal
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal

Geometry - Identifying Corresponding Angles from a Figure
👉 Learn how to identify angles from a figure. This video explains how to solve problems using angle relationships between parallel lines and transversal. We'll determine the solution given, corresponding, alternate interior and exterior. All the angle formed by a transversal with two paral
From playlist Parallel Lines and a Transversal
Learning to Identify Multiple Examples of Corresponding Angles
👉 Learn how to identify angles from a figure. This video explains how to solve problems using angle relationships between parallel lines and transversal. We'll determine the solution given, corresponding, alternate interior and exterior. All the angle formed by a transversal with two paral
From playlist Parallel Lines and a Transversal

Hilbert Space Techniques in Complex Analysis and Geometry (Lecture - 3) by Dror Varolin
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

Hilbert Space Techniques in Complex Analysis and Geometry (Lecture - 2) by Dror Varolin
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

Branched Holomorphic Cartan Geometries by Sorin Dumitrescu
DISCUSSION MEETING ANALYTIC AND ALGEBRAIC GEOMETRY DATE:19 March 2018 to 24 March 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore. Complex analytic geometry is a very broad area of mathematics straddling differential geometry, algebraic geometry and analysis. Much of the interactions be
From playlist Analytic and Algebraic Geometry-2018

Holomorphic Cartan geometries on simply connected manifolds by Sorin Dumitrescu
Discussion Meeting Complex Algebraic Geometry ORGANIZERS: Indranil Biswas, Mahan Mj and A. J. Parameswaran DATE:01 October 2018 to 06 October 2018 VENUE: Madhava Lecture Hall, ICTS, Bangalore The discussion meeting on Complex Algebraic Geometry will be centered around the "Infosys-ICT
From playlist Complex Algebraic Geometry 2018

Mini course 2: Introduction to Higgs bundles (Lecture 2) by Francois Labourie
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017

Dror Varolin - Minicourse - Lecture 1
Dror Varolin Variations of Holomorphic Hilbert spaces Traditional complex analysis focuses on a single space, like a domain in Euclidean space, or more generally a complex manifold, and studies holomorphic maps on that space, into some target space. The typical target space for a domain i
From playlist Maryland Analysis and Geometry Atelier
Overview of gauge theory and submanifold geometry on G_2 manifolds - Simon Donaldson [2014]
Name: Simon Donaldson Event: Program: G2 manifolds Event URL: view webpage Title: Overview of gauge theory and submanifold geometry on G_2 manifolds, I Date: 2014-08-19 @3:30 PM
From playlist Mathematics

Geometry - Identifying Consecutive Interior Angles from a Figure
👉 Learn how to identify angles from a figure. This video explains how to solve problems using angle relationships between parallel lines and transversal. We'll determine the solution given, corresponding, alternate interior and exterior. All the angle formed by a transversal with two paral
From playlist Parallel Lines and a Transversal


